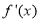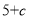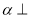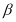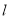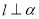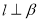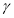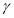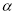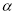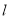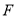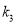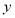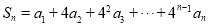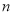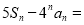题目内容
已知函数 .
.
(1)当 时,
时, 的图象在点
的图象在点 处的切线平行于直线
处的切线平行于直线 ,求
,求 的值;
的值;
(2)当 时,
时, 在点
在点 处有极值,
处有极值, 为坐标原点,若
为坐标原点,若 三点共线,求
三点共线,求 的值.
的值.
(1) ;(2)
;(2)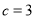 .
.
【解析】
试题分析:(1)本小题考查导数在切线上的应用问题,根据所给的切点及切线所平行的直线方程,可得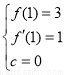 ,从中求解关于
,从中求解关于 的方程组即可;(2)将所给的
的方程组即可;(2)将所给的 代入得
代入得 ,通过求导,先求出函数的极值,写出极值点,然后根据
,通过求导,先求出函数的极值,写出极值点,然后根据 三点共线,利用
三点共线,利用 ,即可计算出
,即可计算出 的值.
的值.
试题解析:(1)当 时,
时,
所以 2分
2分
依题意可得 ,
,
即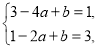 解得
解得 5分
5分
(2)当 时,
时,
所以 7分
7分
令 ,解得
,解得 ,
,
当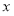 变化时,
变化时, 变化情况如下表:
变化情况如下表:
|
|
|
|
|
|
|
| 0 |
| 0 |
|
|
|
|
|
|
|
所以当 时,
时, ;当
;当 时,
时,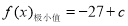
不妨设 8分
8分
因为 三点共线,所以
三点共线,所以
即 ,解得
,解得
故所求 值为
值为 9分.
9分.
考点:1.导数的几何意义;2.函数的极值与导数;3.三点共线的条件.

练习册系列答案
相关题目