题目内容
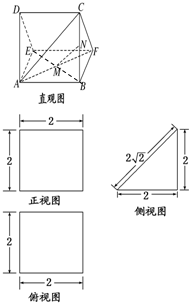 一个多面体的直观图及三视图如图所示,M、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上
一个多面体的直观图及三视图如图所示,M、N分别是AF、BC的中点.请把下面几种正确说法的序号填在横线上①③④
①③④
.①MN∥平面CDEF;
②BE⊥AC;
③该几何体的表面积等于12+4
| 2 |
④该几何体的外接球(几何体的所有顶点都在球面上)的体积等于4
| 3 |
分析:利用三视图以及三视图的数据计算几何体的表面积,外接球的体积,判断直线与平面的平行关系以及直线与直线的垂直.
解答:解:由题意可知几何体是放倒的三棱柱,底面是等腰直角三角形,直角边长为2,高为2的直三棱柱,
即正方体对角面截成的两个三棱柱之一.
M、N分别是AF、BC的中点.所以MN∥EC⇒MN∥平面CDEF,①正确;
EB⊥BC,BE不能垂直MC,所以②不正确;
该几何体的表面积:2×2+2×2+2×
×2×2+2×2
=12+4
,③正确;
该几何体的外接球(几何体的所有顶点都在球面上)的体积,就是棱长为2的正方体的外接球的体积,
外接球的半径为:
×
=
,
外接球的体积:
×(
)3=4
π.④正确.
故答案为:①③④.
即正方体对角面截成的两个三棱柱之一.
M、N分别是AF、BC的中点.所以MN∥EC⇒MN∥平面CDEF,①正确;
EB⊥BC,BE不能垂直MC,所以②不正确;
该几何体的表面积:2×2+2×2+2×
| 1 |
| 2 |
| 2 |
| 2 |
该几何体的外接球(几何体的所有顶点都在球面上)的体积,就是棱长为2的正方体的外接球的体积,
外接球的半径为:
| 1 |
| 2 |
| 22+22+22 |
| 3 |
外接球的体积:
| 4π |
| 3 |
| 3 |
| 3 |
故答案为:①③④.
点评:本题考查三视图与几何体的关系,直线与直线垂直,直线与平面平行,外接球的体积,几何体的表面积,考查空间想象能力,计算能力.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
 18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
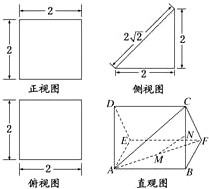 一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).

