题目内容
18、一个多面体的直观图及三视图如图所示，M、N分别是AB1、A1C1的中点．（1）求证：MN⊥AB1，MN∥平面BCC1B1；
（2）求二面角A-BC1-C的余弦值．
分析：（1）要证直线与直线垂直，利用空间直角坐标系，根据坐标求数量积为0即可；
证线与平面平行，证明向量共线即可．
（2）二面角的余弦值，利用三垂线定理，作出二面角的平面角，求解即可．
证线与平面平行，证明向量共线即可．
（2）二面角的余弦值，利用三垂线定理，作出二面角的平面角，求解即可．
解答：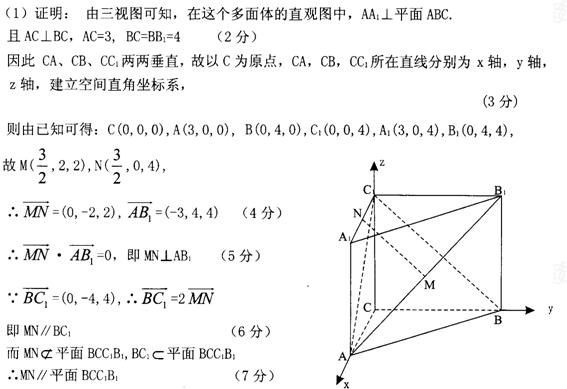
点评：本题考查了学生对空间直角坐标系的运用，二面角的作法，是中档题．
练习册系列答案
相关题目
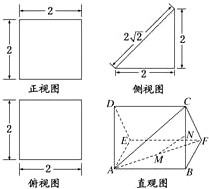一个多面体的直观图及三视图如图所示：（其中M，N分别是AF，BC的中点）．
