题目内容
一个多面体的直观图及三视图如图所示(其中M、N分别是AF、BC的中点),则多面体F-MNB的体积=

| 8 |
| 3 |
| 8 |
| 3 |

分析:由三视图知,该多面体是低面为直角三角形的直三棱柱ADE-BCF,
将多面体F-MNB的体积转化为三棱锥M-BNF,又利用三棱锥M-MNB与三棱锥A-BCF的体积关系求解.
将多面体F-MNB的体积转化为三棱锥M-BNF,又利用三棱锥M-MNB与三棱锥A-BCF的体积关系求解.
解答:解:由三视图知,该多面体是低面为直角三角形的直三棱柱ADE-BCF,

且AB=BC=BF=4,DE=CF=4
,∠CBF=
.
连接BM,FN,∵M、N分别是AF、BC的中点,
∴VM-BNF=
VM-BCF=
×
VA-BCF=
×
×
×BF×BC×AB=
.

且AB=BC=BF=4,DE=CF=4
| 2 |
| π |
| 2 |
连接BM,FN,∵M、N分别是AF、BC的中点,
∴VM-BNF=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 3 |
| 1 |
| 2 |
| 8 |
| 3 |
点评:本题考查了由三视图求几何体的体积问题,考查了学生空间想象能力,转化、运算能力.

练习册系列答案
相关题目
 18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
18、一个多面体的直观图及三视图如图所示,M、N分别是AB1、A1C1的中点.
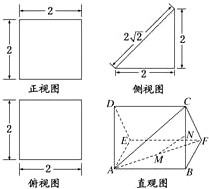 一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点).
