题目内容
已知函数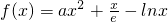 (其中a为常数,e为自然对数的底数).
(其中a为常数,e为自然对数的底数).
(1)任取两个不等的正数x1、x2,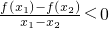 恒成立,求:a的取值范围;
恒成立,求:a的取值范围;
(2)当a>0时,求证:f(x)=0没有实数解.
解: ,
,
 ,
,
∴ ,
,
∵ ,
,
∴ .
.
(2)令g(x)=ax+ (x>0),h(x)=
(x>0),h(x)=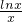 (x>0),当a>0时,f(x)>
(x>0),当a>0时,f(x)> ,h′(x)=
,h′(x)= ,令h′(x)>0,则x∈(0,e),
,令h′(x)>0,则x∈(0,e),
故h(x)在(0,e)上为增函数,(e,+∞)上为减函数,
∴h(x)最大值为:h(e)= ,
,
∴x>0时,g(x)>h(x)恒成立,即ax+ >
>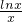 ,
,
即ax2+ -lnx>0恒成立,
-lnx>0恒成立,
∴f(x)=0无解.
分析:(1)先求f'(x)= ,再由:“
,再由:“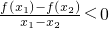 ”得出“f(x)在(0,+∞)上为单调减函数”转化为“f'(x)≤0在(0,+∞)上恒成立”,最后转化为最值法求解.
”得出“f(x)在(0,+∞)上为单调减函数”转化为“f'(x)≤0在(0,+∞)上恒成立”,最后转化为最值法求解.
(2)令g(x)=ax+ (x>0),h(x)=
(x>0),h(x)=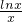 (x>0),当a>0时,f(x)>
(x>0),当a>0时,f(x)> ,h′(x)=
,h′(x)= ,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即ax2+
,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即ax2+ -lnx>0恒成立从而f(x)=0无解.
-lnx>0恒成立从而f(x)=0无解.
点评:本题主要考查函数恒成立问题、用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.
 ,
, ,
,∴
 ,
,∵
 ,
,∴
 .
.(2)令g(x)=ax+
 (x>0),h(x)=
(x>0),h(x)=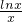 (x>0),当a>0时,f(x)>
(x>0),当a>0时,f(x)> ,h′(x)=
,h′(x)= ,令h′(x)>0,则x∈(0,e),
,令h′(x)>0,则x∈(0,e),故h(x)在(0,e)上为增函数,(e,+∞)上为减函数,
∴h(x)最大值为:h(e)=
 ,
,∴x>0时,g(x)>h(x)恒成立,即ax+
 >
>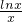 ,
,即ax2+
 -lnx>0恒成立,
-lnx>0恒成立,∴f(x)=0无解.
分析:(1)先求f'(x)=
 ,再由:“
,再由:“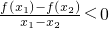 ”得出“f(x)在(0,+∞)上为单调减函数”转化为“f'(x)≤0在(0,+∞)上恒成立”,最后转化为最值法求解.
”得出“f(x)在(0,+∞)上为单调减函数”转化为“f'(x)≤0在(0,+∞)上恒成立”,最后转化为最值法求解.(2)令g(x)=ax+
 (x>0),h(x)=
(x>0),h(x)=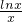 (x>0),当a>0时,f(x)>
(x>0),当a>0时,f(x)> ,h′(x)=
,h′(x)= ,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即ax2+
,令h′(x)>0,可得出h(x)在(0,e)上为增函数,(e,+∞)上为减函数,从而得出h(x)最大值,最终得到即ax2+ -lnx>0恒成立从而f(x)=0无解.
-lnx>0恒成立从而f(x)=0无解.点评:本题主要考查函数恒成立问题、用导数法研究函数的单调性,基本思路是:当函数为增函数时,导数大于等于零;当函数为减函数时,导数小于等于零,已知单调性求参数的范围往往转化为求相应函数的最值问题.

练习册系列答案
相关题目