题目内容
设函数 .
.
(1)求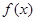 的值域;
的值域;
(2)记 的内角
的内角 的对边长分别为
的对边长分别为 ,若
,若 ,
, ,求
,求 的值.
的值.
(1)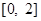 ;(2)
;(2) 或
或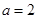 .
.
解析试题分析:本题主要考查两角和的余弦公式、降幂公式、三角函数值域、余弦定理、特殊角的三角函数值等基础知识,考查学生的转化能力、计算能力、数形结合思想.第一问,利用两角和的余弦公式展开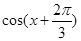 ,用降幂公式化简
,用降幂公式化简 ,最后再一次用两角和的余弦公式将表达式化简成
,最后再一次用两角和的余弦公式将表达式化简成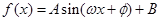 的形式,利用余弦函数的有界性求函数值域;第二问,先利用第一问的结论化简
的形式,利用余弦函数的有界性求函数值域;第二问,先利用第一问的结论化简 ,得到B角的值,在
,得到B角的值,在 中利用余弦定理解a边长.
中利用余弦定理解a边长.
(1)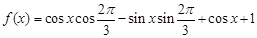
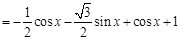

因为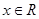 ,所以
,所以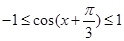 ,
,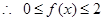
所以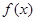 的值域为
的值域为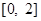 . 6分
. 6分
(2)由 得:
得: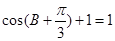 ,即
,即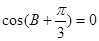 .
.
又因为在 中,
中,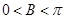 ,故
,故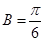 .
.
在 中,由余弦定理得:
中,由余弦定理得: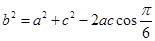
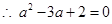 解得:
解得: 或
或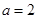 . ………12分
. ………12分
考点:两角和的余弦公式、降幂公式、三角函数值域、余弦定理、特殊角的三角函数值.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
已知函数 (A>0,ω>0)的一系列对应值如下表:
(A>0,ω>0)的一系列对应值如下表:
| x | 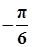 |  | 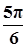 | 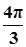 |  |  | 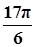 |
| y | -1 | 1 | 3 | 1 | -1 | 1 | 3 |
(1)根据表格提供的数据求函数f(x)的一个解析式;
(2)根据(1)的结果,若函数
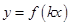 (k>0)周期为
(k>0)周期为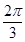 ,当x∈[0,
,当x∈[0, ]时,方程
]时,方程 恰有两个不同的解,求实数m的取值范围;
恰有两个不同的解,求实数m的取值范围;  上的函数
上的函数 的图象关于直线
的图象关于直线 对称,当
对称,当 时函数
时函数 图象如图所示.
图象如图所示.
 的表达式;
的表达式; 的解;
的解; 的值,使得
的值,使得 在
在 上恒成立;若存在,求出
上恒成立;若存在,求出 )随时间
)随时间 (单位:
(单位: )的变化近似满足函数关系;
)的变化近似满足函数关系; .
. ,
, .
. 的最小正周期;
的最小正周期; 上的最大值和最小值.
上的最大值和最小值.  终边所在的象限;
终边所在的象限; (
( ),其图象的两个相邻对称中心的距离为
),其图象的两个相邻对称中心的距离为 .
. 的解析式;
的解析式; 的内角为
的内角为 所对的边分别为
所对的边分别为 (其中
(其中 ),且
),且 ,
,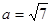 ,
, 面积为
面积为 ,求
,求 的值.
的值. +
+ 的部分图象如图所示.
的部分图象如图所示. 的图象保持纵坐标不变,横坐标向右平移
的图象保持纵坐标不变,横坐标向右平移 个单位后得到函数
个单位后得到函数 的图像,求函数
的图像,求函数 上的值域;
上的值域; 的
的 的取值范围的集合.
的取值范围的集合.
 +α),求下列各式的值:
+α),求下列各式的值: ;
;