题目内容
已知函数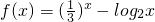 ,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是________.(把你认为正确的命题的序号都填上).
,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是________.(把你认为正确的命题的序号都填上).
①②③
分析:由题意可知f(x)在(0,+∞)单调递减,且0<a<b<c可得f(a)>f(b)>f(c),结合f(a)f(b)f(c)<0可得f(c)<f(b)<f(a)<0或f(c)<0<f(b)<f(a),又f(d)=0课判断a,b,c,d之间的大小
解答:∵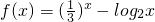 在(0,+∞)单调递减
在(0,+∞)单调递减
∵0<a<b<c
∴f(a)>f(b)>f(c)
∵f(a)f(b)f(c)<0
∴f(c)<f(b)<f(a)<0或f(c)<0<f(b)<f(a)
∵d是函数f(x)的一个即f(d)=0
若f(c)<f(b)<f(a)<0,f(d)=0则可得,c>b>a>d
若f(c)<0<f(b)<f(a),f(d)=0则可得,a<b<d<c
综上可得①d<a可能成立;②d>b可能成立;③d<c可能成立;④d>c不可能成立
故答案为:①②③
点评:本题主要考查了函数的单调性在比较函数的变量与函数值的大小关系中的应用及函数的零点的判断,属于函数知识的简单综合.
分析:由题意可知f(x)在(0,+∞)单调递减,且0<a<b<c可得f(a)>f(b)>f(c),结合f(a)f(b)f(c)<0可得f(c)<f(b)<f(a)<0或f(c)<0<f(b)<f(a),又f(d)=0课判断a,b,c,d之间的大小
解答:∵
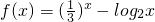 在(0,+∞)单调递减
在(0,+∞)单调递减∵0<a<b<c
∴f(a)>f(b)>f(c)
∵f(a)f(b)f(c)<0
∴f(c)<f(b)<f(a)<0或f(c)<0<f(b)<f(a)
∵d是函数f(x)的一个即f(d)=0
若f(c)<f(b)<f(a)<0,f(d)=0则可得,c>b>a>d
若f(c)<0<f(b)<f(a),f(d)=0则可得,a<b<d<c
综上可得①d<a可能成立;②d>b可能成立;③d<c可能成立;④d>c不可能成立
故答案为:①②③
点评:本题主要考查了函数的单调性在比较函数的变量与函数值的大小关系中的应用及函数的零点的判断,属于函数知识的简单综合.

练习册系列答案
相关题目
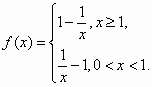
 ,若0<a<b,且f(a)=f(b),则a+2b的取值范围是
,若0<a<b,且f(a)=f(b),则a+2b的取值范围是 (B)
(B) (C)
(C) (D)
(D)
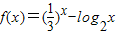 ,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是 .(把你认为正确的命题的序号都填上).
,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是 .(把你认为正确的命题的序号都填上). ,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是( ). (把你认为正确的命题的序号都填上).
,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是( ). (把你认为正确的命题的序号都填上).