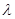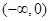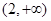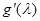Question

（本小题满分12分）

已知函数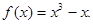

   （I）设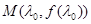是函数图象上的一点，求点M处的切线方程；

   （II）证明过点N（2，1）可以作曲线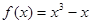的三条切线。

 

Answer 1

【答案】

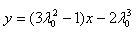（1）（2）略

【解析】（I）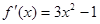

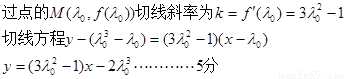
   （II）证明：由（I）知曲线上点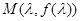处的切线为

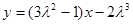
若切线过点N（2，1），则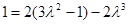

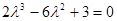
若过N有三条切线等价于方程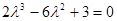有三个不同的解

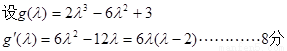
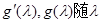变化如下表：

		0	（0，2）	2
	+	0	—	0	+
		极大3		极小—5

在R上只有一个极大值和一个极小值

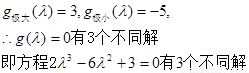
即过点N可以作曲线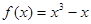的三条切线。 …………12分