题目内容
(本小题满分 分)
分)
已知函数 .(
.( 为常数,
为常数, )
)
(Ⅰ)若 是函数
是函数 的一个极值点,求
的一个极值点,求 的值;
的值;
(Ⅱ)求证:当 时,
时, 在
在 上是增函数;
上是增函数;
(Ⅲ)若对任意的 ,总存在
,总存在 ,使不等式
,使不等式 成立,求实数
成立,求实数 的取值范围.
的取值范围.
(Ⅰ)2
(Ⅱ)证明略
(Ⅲ)
解析 .
.
(Ⅰ)由已知,得  且
且 ,
, ,
, ,
,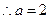 .
.
2分
(Ⅱ)当 时,
时, ,
, ,
, 当
当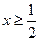 时,
时, .又
.又 ,
, ,故
,故 在
在 上是增函数. 5分
上是增函数. 5分
(Ⅲ) 时,由(Ⅱ)知,
时,由(Ⅱ)知, 在
在 上的最大值为
上的最大值为 ,
,
于是问题等价于:对任意的 ,不等式
,不等式 恒成立.
恒成立.
记 ,(
,( )
)
则 ,
,
当 时,
时, ,
,
 在区间
在区间 上递减,此时,
上递减,此时, ,
,
由于 ,
, 时不可能使
时不可能使 恒成立,故必有
恒成立,故必有 ,
, .
.
若 ,可知
,可知 在区间
在区间 上递减,
上递减,
在此区间上,有 ,与
,与 恒成立矛盾,故
恒成立矛盾,故 ,
,
这时, ,
, 在
在 上递增,恒有
上递增,恒有 ,
,
满足题设要求, ,即
,即 ,
,
所以,实数 的取值范围为
的取值范围为 . 14分
. 14分

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 ,
, 的两个极值点为
的两个极值点为 ,线段
,线段 的中点为
的中点为 .
. 的值;当
的值;当 时,求函数
时,求函数 是定义在
是定义在 上的偶函数,当
上的偶函数,当 时,
时, 为实数).
为实数). 时,求
时,求 ,试判断
,试判断 上的单调性,并证明你的结论;
上的单调性,并证明你的结论; ,使得当
,使得当 有最大值1?若存在,求出
有最大值1?若存在,求出 (a、b、c是常数)是奇函数,且满足
(a、b、c是常数)是奇函数,且满足 .
. )上的单调性并证明.
)上的单调性并证明. 都满足不等式
都满足不等式 的所有函数
的所有函数 组成的集合记为M,例如,函数
组成的集合记为M,例如,函数 。
。 ,证明:
,证明: ;
; ,并说明理由;
,并说明理由;
 的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的
的时候小白鼠将死亡.但注射某种药物,将可杀死此时其体内该病毒细胞的 .
.
 ,
, )
)
 的最大值和最小正周期;
的最大值和最小正周期;  三个内角,若,
三个内角,若, ,且C为锐角,求
,且C为锐角,求

 是同时满足下列两个性质的函数
是同时满足下列两个性质的函数 组成的集合:
组成的集合: ,使得
,使得 .
. 是否属于集合
是否属于集合
 ,求实数
,求实数 的取值范围.
的取值范围.