题目内容
如图所示,在正三棱锥S—ABC中,M、N分别是SC、BC的中点,且 ,若侧棱
,若侧棱 则正三棱锥S—ABC外接球的表面积是 ( )
则正三棱锥S—ABC外接球的表面积是 ( )

A.12π B.32π
C.36π D.48π
 ,若侧棱
,若侧棱 则正三棱锥S—ABC外接球的表面积是 ( )
则正三棱锥S—ABC外接球的表面积是 ( )
A.12π B.32π
C.36π D.48π
C
本题考查空间位置关系的论证及球的有关知识。
据已知可得SB⊥AM,又在正三棱锥中易知SB⊥AC,故SB⊥平面SAC,从而SB⊥SA,故正三棱锥是侧棱两两垂直且边长为
 ,其可视为球的内接边长为
,其可视为球的内接边长为 的正方体从同一顶点引出的三条棱构成的几何体,由于其体对角线即为球的直径即:(
的正方体从同一顶点引出的三条棱构成的几何体,由于其体对角线即为球的直径即:( )2·3=(2R)2
)2·3=(2R)2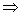 4R2=36
4R2=36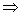 S球=4πR2=36π。故选C。
S球=4πR2=36π。故选C。
练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
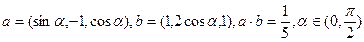
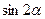 及
及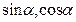 的值;
的值;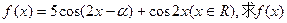 的最小正周期及
的最小正周期及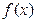 取得最大值时x的值。
取得最大值时x的值。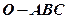 中,
中,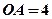 ,
,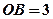 ,
,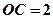 ,且
,且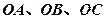 两两垂直,
两两垂直,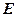 是
是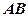 中点,
中点,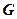 是
是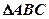 重心,现如图建立空间直角坐标系
重心,现如图建立空间直角坐标系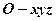 。
。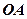 和
和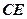 所成角的余弦值。
所成角的余弦值。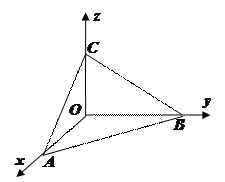
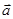 =(1,x,2),
=(1,x,2),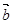 =(2,1,2),且
=(2,1,2),且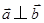 ,则x=_____▲_____.
,则x=_____▲_____.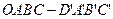 中,
中,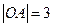 ,
,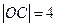 ,
,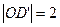 .写出
.写出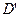 ,
,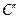 ,
,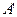 ,
,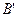 四点的坐标.
四点的坐标.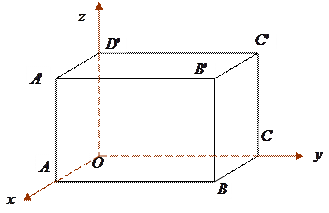
 是两个非零向量,且
是两个非零向量,且 ,则
,则 与
与 的夹角为( )
的夹角为( )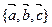 是空间一个
是空间一个 基底,则一定可以与向量
基底,则一定可以与向量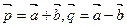
 构成空间的另一个基底的向量是
构成空间的另一个基底的向量是



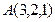 、
、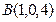 ,则线段AB的中点P的坐标为 ( )
,则线段AB的中点P的坐标为 ( )



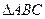 中,已知
中,已知 ,
,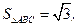 则
则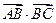 的值为 .
的值为 .