Question

有一个正四棱锥，它的底面边长与侧棱长均为a，现用一张正方形包装纸将其完全包住（不能裁剪纸，但可以折叠），那么包装纸的最小边长应为（　　）

A． 2 + 6 2 a

B．( 2 + 6 )a

C． 1+ 3 2 a

D．(1+ 3 )a

Answer 1

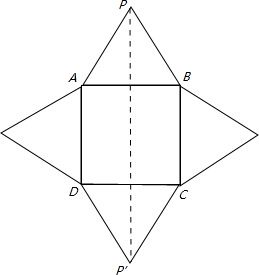
由题意可知：当正四棱锥沿底面将侧面都展开时如图所示：
分析易知当以PP′为正方形的对角线时，
所需正方形的包装纸的面积最小，此时边长最小．
设此时的正方形边长为x则：（PP′）²=2x²，
又因为 PP′=a+2×

3

2

a=a+

3

a，
∴( a+

3

a)2=2x2，
解得：x=

6 + 2

2

a．
故选A