题目内容
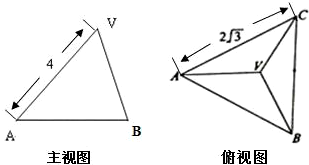已知正三棱锥V-ABC的主视图，俯视图如图所示，其中VA=4，AC=2| 3 |
| A、9 | ||
| B、6 | ||
C、3
| ||
D、
|
分析：由题意可知，几何体的侧面是等腰三角形，要该三棱锥的左视图的面积，必须求出VA在左视图的射影的长度，即求V到底面的距离．
解答：解：正三棱锥V-ABC的侧面是等腰三角形，底面是正三角形，底面上的高是3，
所以V到底面的距离：
=2
；
该三棱锥的左视图的面积：
×2
×2
=6
故选C．
所以V到底面的距离：
| 42-22 |
| 3 |
该三棱锥的左视图的面积：
| 1 |
| 2 |
| 3 |
| 3 |
故选C．
点评：本题考查三视图求面积，空间想象能力，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
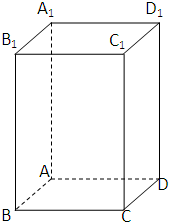
已知：在正四棱柱A1B1C1D1-ABCD中，棱AB=2，棱BB1=4，点M是棱DD1中点
，其主视图和俯视图如下图所示，则其左视图的面积是 ．
