题目内容
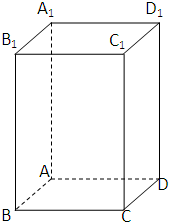
已知：在正四棱柱A1B1C1D1-ABCD中，棱AB=2，棱BB1=4，点M是棱DD1中点（I）求三棱锥C1-ACM的体积V；
（Ⅱ）求点C1到平面ACM的距离．
【答案】分析：（I）利用
=
，即可求得结论；
（II）利用体积公式，结合（I）的结论，可求点C1到平面ACM的距离．
解答：解：（I）由题意，
=
=
=
=
；
（II）设点C1到平面ACM的距离为h，则
△ACM中，AC=MA=MC=
，∴S△ACM=
=
∴
∴
．
点评：本题考查三棱锥体积公式，考查学生分析解决问题的能力，属于昨天的．
=，即可求得结论；（II）利用体积公式，结合（I）的结论，可求点C1到平面ACM的距离．
解答：解：（I）由题意，
====；（II）设点C1到平面ACM的距离为h，则
△ACM中，AC=MA=MC=
，∴S△ACM==∴
∴
．点评：本题考查三棱锥体积公式，考查学生分析解决问题的能力，属于昨天的．
练习册系列答案
名校课堂系列答案
相关题目
已知：在正四棱柱A1B1C1D1-ABCD中，棱AB=2，棱BB1=4，点M是棱DD1中点