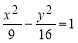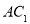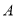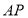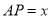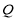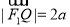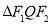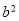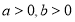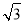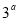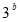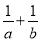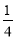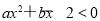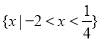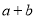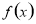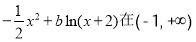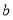题目内容
已知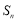 是等比数列
是等比数列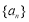 的前
的前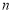 项和,
项和,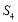 、
、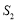 、
、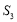 成等差数列,且
成等差数列,且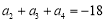 .
.
(1)求数列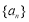 的通项公式;
的通项公式;
(2)是否存在正整数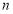 ,使得
,使得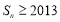 ?若存在,求出符合条件的所有
?若存在,求出符合条件的所有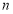 的集合;若不存在,说明理由.
的集合;若不存在,说明理由.
(1)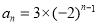 ;(2)存在符合条件的正整数
;(2)存在符合条件的正整数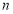 的集合为
的集合为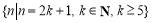 .
.
【解析】
试题分析:(1)设数列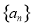 的公比为
的公比为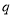 ,依题意,列出关于首项
,依题意,列出关于首项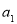 与公比
与公比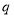 的方程组,解之即可求得数列
的方程组,解之即可求得数列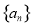 的通项公式;(2)依题意,可得
的通项公式;(2)依题意,可得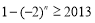 ,对
,对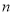 的奇偶性进行分类讨论,即可求得答案.
的奇偶性进行分类讨论,即可求得答案.
试题解析:(1)【解析】
设数列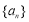 的公比为
的公比为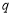 ,则
,则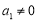 ,
,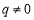
由题意得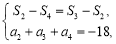 即
即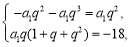 解得
解得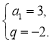
故数列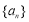 的通项公式为
的通项公式为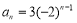 6分
6分
(2)由(1)有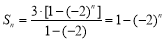 7分
7分
若存在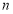 ,使得
,使得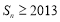 ,则
,则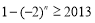 ,即
,即 8分
8分
当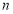 为偶数时,
为偶数时,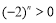 ,上式不成立 9分
,上式不成立 9分
当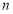 为奇数时,
为奇数时,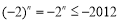 ,即
,即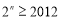 ,则
,则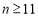 11分
11分
综上,存在符合条件的正整数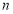 的集合为
的集合为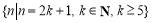 12分.
12分.
考点:1.等比数列;2.等差数列;3.数列的求和.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目