题目内容
求函数
的定义域、值域和单调区间.
解析:注意到对数函数的图象及性质和复合函数的单调性.
答案:由μ(x)=x2-5x+4＞0,解得x＞4或x＜1,?
所以x∈(-∞,1)∪(4,+∞).?
当x∈(-∞,1)∪(4,+∞)时,{μ|μ=x2-5x+4}=R +,
所以函数的值域是R +.
因为函数是由
与μ(x)=x2-5x+4复合而成,函数
在其定义域上是单调递减的,函数μ(x)=x 2-5x+4在(-∞,
)上为减函数,在［
,+∞)上为增函数.考虑到函数的定义域及复合函数单调性,
的增区间是定义域内使
为减函数、μ(x)=x 2-5x+4也为减函数的区间,即(-∞,1); 
的减区间是定义域内使
为减函数、μ(x)=x 2-5x+4为增函数的区间,即(4,+∞).
练习册系列答案
阅读快车系列答案
相关题目
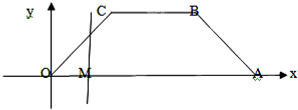如图，等腰梯形OABC，底角为45°，各顶点的坐标分别为O（0，0），A（6，0），B（4，2），C（2，2）．一条与y轴平行的动直线l从O点开始做平行移动，到A点为止．设直线l与x轴的交点M，记OM=x，记梯形被直线l截得的在l左侧的图形面积为y．
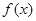的图象经过点
.
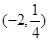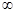）上是减函数.