题目内容

已知函数f(x)=loga(a－ax)且a＞1，

（1）求函数的定义域和值域；

（2）讨论f(x)在其定义域上的单调性；

（3）证明函数图象关于y=x对称．

 

【答案】

（1）定义域为(－∞，1)，值域为(－∞，1)；

（2）f(x)在定义域(－∞，1)上是减函数；（3）见解析。

【解析】主要考查对数函数的图象和性质，复合函数的单调性。

解：(1)定义域为(－∞，1)，值域为(－∞，1)

(2)设1＞x2＞x1

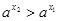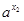∵a＞1，∴，于是a－＜a－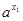

则loga(a－a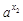)＜loga(a－)

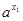即f(x2)＜f(x1)

∴f(x)在定义域(－∞，1)上是减函数

(3)证明：令y=loga(a－ax)(x＜1)，则a－ax=ay，x=loga(a－ay)

∴f－1(x)=loga(a－ax)(x＜1)

故f(x)的反函数是其自身，得函数f(x)=loga(a－ax)(x＜1＝图象关于y=x对称．

 

 

练习册系列答案
相关题目
已知函数f(x)=
1
3
x3-
3
2
ax2-(a-3)x+b
（1）若函数f（x）在P（0，f（0））的切线方程为y=5x+1，求实数a，b的值：
（2）当a＜3时，令g(x)=
f′(x)
x
，求y=g（x）在[l，2]上的最大值．
已知函数f(x)=
1
2
x2-alnx的图象在点P（2，f（2））处的切线方程为l：y=x+b
（1）求出函数y=f（x）的表达式和切线l的方程；
（2）当x∈[
1
e
，e]时（其中e=2.71828…），不等式f（x）＜k恒成立，求实数k的取值范围．
已知函数f(x)=lnx，g(x)=
12
x2+a（a为常数），直线l与函数f（x）、g（x）的图象都相切，且l与函数f（x）的图象的切点的横坐标为1．
（1）求直线l的方程及a的值；
（2）当k＞0时，试讨论方程f（1+x2）-g（x）=k的解的个数．
已知函数f(x)=
13
x3+x2+ax．
（1）讨论f（x）的单调性；
（2）设f（x）有两个极值点x1，x2，若过两点（x1，f（x1）），（x2，f（x2））的直线l与x轴的交点在曲线y=f（x）上，求a的值．
已知函数f(x)=x3-
32
ax2+b，a，b为实数，x∈R，a∈R．
（1）当1＜a＜2时，若f（x）在区间[-1，1]上的最小值、最大值分别为-2、1，求a、b的值；
（2）在（1）的条件下，求经过点P（2，1）且与曲线f（x）相切的直线l的方程；
（3）试讨论函数F（x）=（f′（x）-2x2+4ax+a+1）•ex的极值点的个数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网