题目内容
设函数
图像的一条对称轴是直线
。
（Ⅰ）求
；
（Ⅱ）求函数
的单调增区间；
（Ⅲ）证明直线
与函数的图像不相切。
(Ⅰ)
sin(2×
+
)=±1,∴
+=kπ+
,k∈Z.
∵－π<<0,∴=－
.
(Ⅱ)解：由（Ⅰ）知=－，因此
y=sin(2x－).
由题意得
2kπ－≤2x－≤2kπ+,k∈Z.
所以函数y=sin(2x－)的单调增区间为[kπ+, kπ+
],k∈Z.
(Ⅲ)证明：∵|y′|=|（sin(2x－)′|=|2cos(2x－)|≤2,
所以曲线y=f(x)的切线斜率取值范围为[－2,2].而直线5x－2y+c=0的斜率为
>2,
所以直线5x－2y+c=0与函数y=sin(2x－)的图像不相切.
练习册系列答案
新活力总动员暑系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
图像的一条对称轴是直线
．
；
的单调增区间；
于函数
图像的一条对称轴是直线
。
；
的单调增区间；
上的图像。
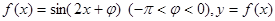图像的一条对称轴是直线
.
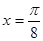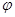；（2）画出函数
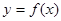在区间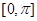
上的图像（在答题纸上完成列表并作图）.
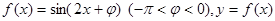图像的一条对称轴是直线
。
；
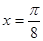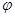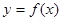的单调增区间；
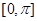上的图像。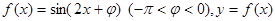
图像的一条对称轴是直线
；
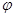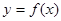的单调区间及最值；