题目内容
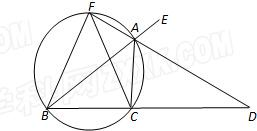 如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.
如图,已知AD是△ABC的外角∠EAC的平分线,交BC的延长线于点D,延长DA交△ABC的外接圆于点F,连接FB、FC.(1)求证:FB=FC;
(2)求证:FB2=FA•FD;
分析:(I)根据角平分线得到两个角相等,根据圆内接四边形得到四边形的一个外角等于不相邻的一个内角,得到两个角相等,根据同弧所对的圆周角相等和对顶角相等,根据等量代换得到∠FBC=∠FCB,三角形是一个等腰三角形,得到两边相等.
(II)根据两个三角形对应角相等,得到两个三角形相似,根据相似三角形对应边成比例,得到比例式,不比例式化成乘积式,得到结果.
(II)根据两个三角形对应角相等,得到两个三角形相似,根据相似三角形对应边成比例,得到比例式,不比例式化成乘积式,得到结果.
解答: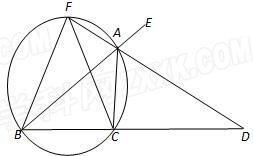 解:(Ⅰ)∵AD平分∠EAC,
解:(Ⅰ)∵AD平分∠EAC,
∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,
∴FB=FC.
(Ⅱ)∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD,
∴△FBA∽△FDB.
∴
=
,
∴FB2=FA•FD.
 解:(Ⅰ)∵AD平分∠EAC,
解:(Ⅰ)∵AD平分∠EAC,∴∠EAD=∠DAC.
∵四边形AFBC内接于圆,
∴∠DAC=∠FBC.
∵∠EAD=∠FAB=∠FCB,
∴∠FBC=∠FCB,
∴FB=FC.
(Ⅱ)∵∠FAB=∠FCB=∠FBC,∠AFB=∠BFD,
∴△FBA∽△FDB.
∴
| FB |
| FD |
| FA |
| FB |
∴FB2=FA•FD.
点评:本题考查圆内接四边形的性质,考查相似三角形的判定和性质,考查圆周角定理,考查对顶角相等,是一个基础题.

练习册系列答案
相关题目
 选修4-1:几何证明选讲
选修4-1:几何证明选讲 如图,已知ABCD是底角为30°的等腰梯形,AD=2
如图,已知ABCD是底角为30°的等腰梯形,AD=2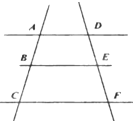 如图,已知AD∥BE∥CF,下列比例式成立的是( )
如图,已知AD∥BE∥CF,下列比例式成立的是( ) 如图,已知长方体ABCD-A′B′C′D′中,AB=2
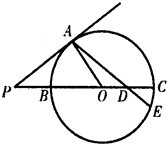
如图,已知长方体ABCD-A′B′C′D′中,AB=2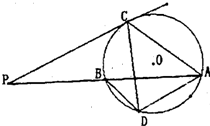 (2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,
(2011•洛阳二模)如图,已知PBA是圆O的割线,PC是圆的切线,