题目内容
2.甲、乙两人相约在某天的7点至8点之间见面,双方共同约定早到者等候15分钟,若另一方仍未到,可自行离去,假设甲、乙两人在7点到8点的任意时间到达的概率是等可能的,求甲、乙两人约会成功的概率.分析 从晚上7点开始计时,设甲经过x分钟到达,乙经过y分钟到达,可得x、y满足的不等式线组对应的平面区域为如图的正方形OBDF,而甲乙能够见面,x、y满足的平面区域是图中的六边形OACDE.分别算出图中正方形和六边形的面积,相除即可得到两人能见面的概率.
解答 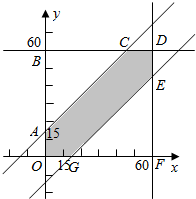 解:从晚上7点开始计时,设甲经过x分钟到达,乙经过y分钟到达,
解:从晚上7点开始计时,设甲经过x分钟到达,乙经过y分钟到达,
则x、y满足$\left\{\begin{array}{l}{0≤x≤60}\\{0≤y≤60}\end{array}\right.$,作出不等式组对应的平面区域,
得到图中的正方形OABC,
若甲乙能够见面,则x、y满足|x-y|≤15,
该不等式对应的平面区域是图中的六边形OACDEF,
则G(15,0),E(60,45),F(60,0),
则S△GEF=$\frac{1}{2}×45×45=\frac{45×45}{2}$
S正方形OFDC=60×60=3600,
S六边形OACDEF=S正方形OBDF-2S△GEF=3600-45×45=1575,
因此,甲乙能见面的概率P=$\frac{1575}{3600}$=$\frac{7}{16}$
点评 本题主要考查概率的计算,根据几何概型的概率公式,结合线性规划求出对应区域的面积是解决本题的关键.

练习册系列答案
相关题目
12.若x∈(1,e),a=ln x,b=(ln x)2,c=ln(ln x),则a,b,c的大小关系为( )
| A. | c>b>a | B. | b>c>a | C. | a>b>c | D. | b>a>c |
 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,△VAB为等边三角形,AC⊥BC且AC=BC=$\sqrt{2}$,O、M分别为AB、VA的中点.