题目内容
给出下列命题:
①若y=f(x)是奇函数,则y=|f(x)|的图象关于y轴对称;
②若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则8是函数f(x)的一个周期;
③若logm3<logn3<0,则0<m<n<1;
④若f(x)=e|x-a|在[1,+∞)上是增函数,则a≤1.
其中正确命题的序号是
①若y=f(x)是奇函数,则y=|f(x)|的图象关于y轴对称;
②若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则8是函数f(x)的一个周期;
③若logm3<logn3<0,则0<m<n<1;
④若f(x)=e|x-a|在[1,+∞)上是增函数,则a≤1.
其中正确命题的序号是
①②④
①②④
.分析:①根据函数奇偶性的性质进行判断.②根据函数周期性的定义进行推导.③根据对数的运算法则进行计算.④根据复合函数的单调性进行判断.
解答:解:①若y=f(x)是奇函数,则f(-x)=-f(x),∴|f(-x)|=|-f(x)|=|f(x)|,即|f(x)|为偶函数,∴图象关于y轴对称;正确.
②若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则f(x)≠0,
∴f(x)•f(x+4)=f(x+4)•f(x+8)=1,即f(x+8)=f(x),则8是函数f(x)的一个周期;正确.
③若logm3<logn3<0,则
<
<0,
即log3n<log3m<0,即0<n<m<1,∴③错误.
④设t=|x-a|,则函数y=et单调递增,t=|x-a|在[a,+∞)上也单调递增,∴若f(x)=e|x-a|在[1,+∞)上是增函数,则a≤1.正确.
∴正确的是①②④.
故答案为:①②④.
②若函数f(x)对任意x∈R满足f(x)•f(x+4)=1,则f(x)≠0,
∴f(x)•f(x+4)=f(x+4)•f(x+8)=1,即f(x+8)=f(x),则8是函数f(x)的一个周期;正确.
③若logm3<logn3<0,则
| 1 |
| log3m |
| 1 |
| log3n |
即log3n<log3m<0,即0<n<m<1,∴③错误.
④设t=|x-a|,则函数y=et单调递增,t=|x-a|在[a,+∞)上也单调递增,∴若f(x)=e|x-a|在[1,+∞)上是增函数,则a≤1.正确.
∴正确的是①②④.
故答案为:①②④.
点评:本题主要考查函数奇偶性,周期性和单调性的判断和应用,利用相应的定义和性质是解决本题的关键,要求熟练掌握函数的性质的综合应用.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案
相关题目
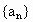 成等比数列,
成等比数列,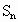 是前n项和,则
是前n项和,则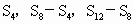 成等比数列;
成等比数列;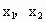 ,若
,若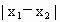 的最小值为π,则ω的值为2,θ的值为
的最小值为π,则ω的值为2,θ的值为 ;
;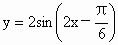 的图象的一个对称点是
的图象的一个对称点是 .
.