题目内容
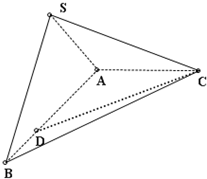
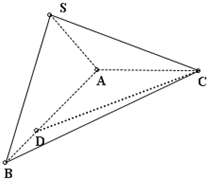
如图所示，在三棱锥S－ABC中，SA⊥底面ABC，底面ABC为正三角形，AH⊥面SBC．求证：H不可能是△SBC的垂心．
答案：
解析：
解析：
|
证明：假设H是△SBC的垂心，则BH⊥SC． 又∵AH⊥面SBC，即AH⊥SC，∴SC⊥平面AHB．则SC⊥AB． 又∵SA⊥平面ABC，即SA⊥AB，则AB⊥平面SAC，∴AB⊥AC．这与∠BAC＝60°矛盾，∴假设不成立．故H不可能是△SBC的垂心． |
练习册系列答案
初中学业考试导与练系列答案
相关题目
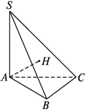
如图所示，在三棱锥S-ABC中，平面SAB⊥平面ABC，AC⊥AB，SA=SB=AB=2，AC=1（1）求异面直线AB与SC所成的角的余弦值；
（2）在线段AB上求一点D，使CD与平面SAC成45°角．
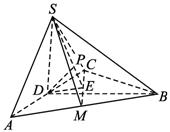
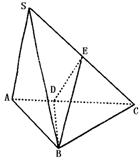如图所示，在三棱锥S—ABC中，SA⊥底面ABC，AB⊥BC，DE垂直平分SC，且分别交AC、SC于D、E.又SA＝AB，SB＝SC.求以BD为棱，以BDE与BDC为面的二面角的度数.
,M为AB的中点.