题目内容
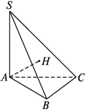
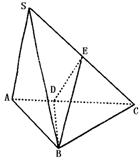 如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
解析:
解法一:由于SB=BC,且E是SC中点,因此BE是等腰三角形SBC的底边SC的中线,所以SC⊥BE.又已知SC⊥DE,BE∩DE=E,
∴SC⊥平面BDE,∴SC⊥BD,
又∵SA⊥底面ABC,BD在底面ABC上,∴SA⊥BD.
而SA∩SC=S,所以BD⊥平面SAC.
∵DE=平面SAC∩平面BDE,DC=平面SAC∩平面BDC,
∴BD⊥DE,BD⊥DC.∴∠EDC是所求二面角的平面角.
∵SA⊥底面ABC,∴SA⊥AB,SA⊥AC.
设SA=a,则AB=a,BC=SB=![]() a.
a.
又AB⊥BC,所以AC=![]() a.在RtΔSAC中tg∠ACS=
a.在RtΔSAC中tg∠ACS=![]() =
=![]() ,所以∠ACS=30°.
,所以∠ACS=30°.
又已知DE⊥SC,所以∠EDC=60°,即所求的二面角等于60°.
解法二:由于SB=BC,且E是SC的中点,因此BE是等腰ΔSBC的底边SC的中线,所以SC⊥BE.又已知SC⊥DE,BE∩DE=E.∴SC⊥平面BDE,SC⊥BD.
由于SA⊥底面ABC,且A是垂足,所以,AC是SC在平面ABC上的射影,由三垂线定理的逆定理得BD⊥AC;又E∈SC,AC是SC在平面内的射影,所以E在平面ABC内的射影在AC上,由于D∈AC,所以DE在平面ABC内的射影在AC上,根据三垂线定理得BD⊥DE.
∵DE![]() 平面BDE,DC
平面BDE,DC![]() 平面BDC.∴∠EDC是所求二面角的平面角.以下解法同解法一.
平面BDC.∴∠EDC是所求二面角的平面角.以下解法同解法一.

练习册系列答案
相关题目
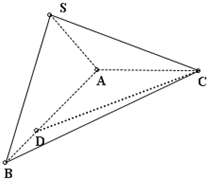 如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1
如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1(1)求异面直线AB与SC所成的角的余弦值;
(2)在线段AB上求一点D,使CD与平面SAC成45°角.