题目内容
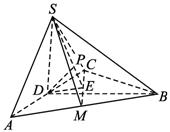
如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1
(1)求异面直线AB与SC所成的角的余弦值;
(2)在线段AB上求一点D,使CD与平面SAC成45°角.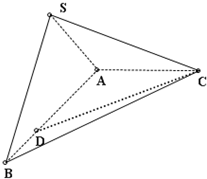
(1)求异面直线AB与SC所成的角的余弦值;
(2)在线段AB上求一点D,使CD与平面SAC成45°角.

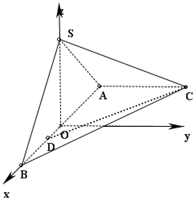
(1)取AB的中点O,连接OS,则有OS⊥AB
又∵平面SAB⊥平面ABC,
∴OS⊥平面ABC …(2分)
∴以AB为x轴,OS为z轴,过O作AC的平行线为y轴,如图,建立空间直角坐标系O-xyz.
∵A(-1,0,0),B(1,0,0),C(-1,1,0),
S(0,0,
| 3 |
∴
| AB |
| SC |
| 3 |
∴cos<
| AB |
| SC |
| ||||
|
|
| -2 | ||
2×
|
| ||
| 5 |
又异面直线AB与SC所成角大于0,小于等于
| π |
| 2 |
| ||
| 5 |
(2)依题意可设D(a,0,0),其中a∈[-1,1],
∴
| CD |
设平面SAC的法向量为
| n |
∵
| SA |
| 3 |
| AC |
∴
|
| n |
| 3 |
设CD与平面SAC所成的角为θ,则sinθ=|cos<
| CD |
| n |
| ||
|
| ||
| 2 |
∴
| 3 |
| 2• |
| a2+2a+2 |
两边同平方,化简得a2+2a-1=0
∴a=-1-
| 2 |
| 2 |
所以满足条件的点D的坐标为(
| 2 |

练习册系列答案
相关题目
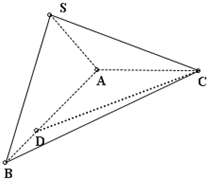 如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1
如图所示,在三棱锥S-ABC中,平面SAB⊥平面ABC,AC⊥AB,SA=SB=AB=2,AC=1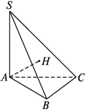
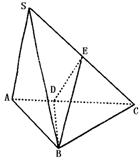 如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.
如图所示,在三棱锥S—ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC、SC于D、E.又SA=AB,SB=SC.求以BD为棱,以BDE与BDC为面的二面角的度数.