题目内容
已知函数f(x)=Asin(3x+φ) ( A>0,x∈(-∞,+∞),0<φ<π ) 在x= 时取得最大值4.
时取得最大值4.(1)求函数f(x)的最小正周期及解析式;
(2)求函数f(x)的单调增区间;
(3)求函数f(x)在
 上的值域.
上的值域.
【答案】分析:(1)根据y=Asin(ωx+∅)的最小正周期的求法求得此函数的最小正周期.由函数的最大值求A,根据函数在x= 时取得最大值4,求得φ,从而得到函数的解析式.
时取得最大值4,求得φ,从而得到函数的解析式.
(2)令2kπ-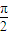 ≤3x+
≤3x+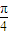 ≤2kπ+
≤2kπ+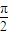 ,k∈z,求得x的范围,即可到函数f(x)的单调增区间.
,k∈z,求得x的范围,即可到函数f(x)的单调增区间.
(3)根据x∈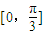 ,结合正弦函数的定义域和值域,求得函数f(x)在
,结合正弦函数的定义域和值域,求得函数f(x)在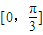 上的值域.
上的值域.
解答:解:(1)∵函数f(x)=Asin(3x+φ),故函数的最小正周期为T= .
.
由函数的最大值为4可得A=4,
由函数在x=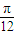 时取得最大值4可得 4sin(3×
时取得最大值4可得 4sin(3×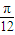 +φ)=4,故
+φ)=4,故 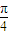 +φ=2kπ+
+φ=2kπ+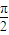 ,k∈z.
,k∈z.
结合0<φ<π,可得 φ=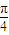 .
.
综上,函数f(x)=4sin(3x+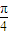 ).
).
(2)令2kπ-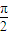 ≤3x+
≤3x+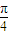 ≤2kπ+
≤2kπ+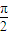 ,k∈z,求得≤
,k∈z,求得≤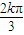 -
-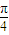 ≤x≤
≤x≤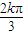 +
+ ,
,
故函数f(x)的单调增区间为[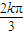 -
-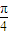 ,
,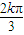 +
+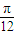 ],k∈z.
],k∈z.
(3)∵x∈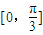 ,∴3x+
,∴3x+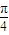 ∈[
∈[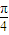 ,
,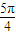 ],∴sin(3x+
],∴sin(3x+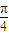 )∈[-
)∈[-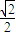 ,1],
,1],
故4sin(3x+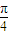 )∈[-2
)∈[-2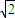 ,4].
,4].
故函数f(x)在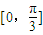 上的值域为[-2
上的值域为[-2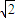 ,4].
,4].
点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的最小正周期、单调性、定义域和值域,属于中档题.
 时取得最大值4,求得φ,从而得到函数的解析式.
时取得最大值4,求得φ,从而得到函数的解析式.(2)令2kπ-
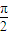 ≤3x+
≤3x+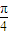 ≤2kπ+
≤2kπ+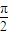 ,k∈z,求得x的范围,即可到函数f(x)的单调增区间.
,k∈z,求得x的范围,即可到函数f(x)的单调增区间.(3)根据x∈
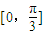 ,结合正弦函数的定义域和值域,求得函数f(x)在
,结合正弦函数的定义域和值域,求得函数f(x)在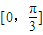 上的值域.
上的值域.解答:解:(1)∵函数f(x)=Asin(3x+φ),故函数的最小正周期为T=
 .
.由函数的最大值为4可得A=4,
由函数在x=
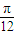 时取得最大值4可得 4sin(3×
时取得最大值4可得 4sin(3×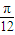 +φ)=4,故
+φ)=4,故 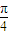 +φ=2kπ+
+φ=2kπ+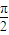 ,k∈z.
,k∈z.结合0<φ<π,可得 φ=
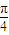 .
.综上,函数f(x)=4sin(3x+
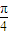 ).
).(2)令2kπ-
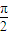 ≤3x+
≤3x+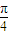 ≤2kπ+
≤2kπ+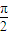 ,k∈z,求得≤
,k∈z,求得≤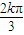 -
-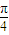 ≤x≤
≤x≤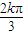 +
+ ,
,故函数f(x)的单调增区间为[
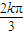 -
-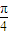 ,
,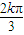 +
+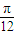 ],k∈z.
],k∈z.(3)∵x∈
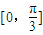 ,∴3x+
,∴3x+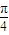 ∈[
∈[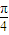 ,
,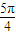 ],∴sin(3x+
],∴sin(3x+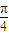 )∈[-
)∈[-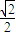 ,1],
,1],故4sin(3x+
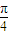 )∈[-2
)∈[-2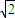 ,4].
,4].故函数f(x)在
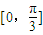 上的值域为[-2
上的值域为[-2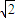 ,4].
,4].点评:本题主要考查由函数y=Asin(ωx+∅)的部分图象求解析式,函数y=Asin(ωx+∅)的最小正周期、单调性、定义域和值域,属于中档题.

练习册系列答案
 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目