题目内容
(本小题满分14分)
已知函数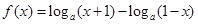 ,(a>0,且a≠1).(1)求函数f(x)的定义域;
,(a>0,且a≠1).(1)求函数f(x)的定义域;
(2)判断函数f(x)的奇偶性,并说明理由;(3)设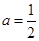 ,解不等式f(x)>0.
,解不等式f(x)>0.
已知函数
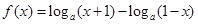 ,(a>0,且a≠1).(1)求函数f(x)的定义域;
,(a>0,且a≠1).(1)求函数f(x)的定义域;(2)判断函数f(x)的奇偶性,并说明理由;(3)设
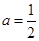 ,解不等式f(x)>0.
,解不等式f(x)>0.解:(1)由题知:
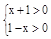 ,
,解得:-1<x<1,所以函数f(x)的定义域为(-1,1)。…………………………………4分
(2)奇函数。
证明:因为函数f(x)的定义域为(-1,1),所以对任意x∈(-1,1),
f(-X)=loga(-x+1)-loga(1-(-x))=-[loga(x+1)-loga(1-x)]=-f(x)
所以函数f(x)是奇函数。…………………………………8分
(3)由题知:
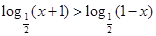 ,即有
,即有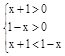 ,解得:-1<x<0,所以不等式f(x)>0的解集为{x|-1<x<0} ………………………………14分
,解得:-1<x<0,所以不等式f(x)>0的解集为{x|-1<x<0} ………………………………14分略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
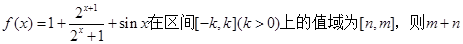 等于
等于 ,
, ,
, ,实数a满足
,实数a满足 >0,那么当x>1时必有( )
>0,那么当x>1时必有( ) <
< <
<
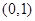 上的函数
上的函数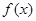 ,对任意的
,对任意的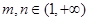 且
且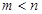 时,都有
时,都有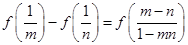 .记
.记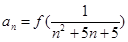 ,
,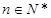 ,则在数列
,则在数列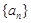 中,
中,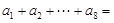
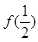
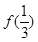
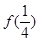
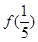
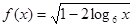 的定义域为
的定义域为 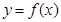 满足
满足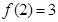 ,且对任意
,且对任意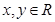 都有
都有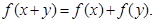
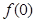 的值并证明函数
的值并证明函数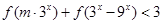 对任意
对任意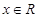 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。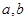 ,可按规则
,可按规则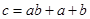 扩充为一个新数
扩充为一个新数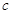 ,在
,在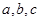 三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.
三个数中取两个较大的数,按上述规则扩充得到一个新数,依次下去,将每扩充一次得到一个新数称为一次操作.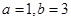 ,按上述规则操作三次,扩充所得的数是__________;
,按上述规则操作三次,扩充所得的数是__________;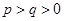 ,经过6次操作后扩充所得的数为
,经过6次操作后扩充所得的数为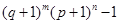 (
(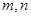 为正整数),则
为正整数),则