题目内容
为了在夏季降温和冬季供暖时减少能源消耗,房屋的屋顶和外墙需要建造隔热层,某栋建筑物要建造可使用20年的隔热层,每厘米厚的隔热层建造成本为6万元.该建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度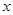 (单位:
(单位: )满足关系:
)满足关系:
若不建隔热层,每年能源消耗费用为8万元。设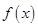 为隔热层建造费用与20年的能源消耗费用之和。
为隔热层建造费用与20年的能源消耗费用之和。
(Ⅰ)求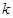 的值及
的值及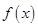 的表达式;
的表达式;
(Ⅱ)隔热层修建多厚时,总费用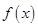 最小,并求最小值.
最小,并求最小值.
(Ⅰ)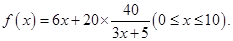 ;(Ⅱ)当
;(Ⅱ)当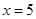 时,最小值为70.
时,最小值为70.
解析试题分析:(Ⅰ)由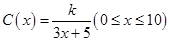 ,及若不建隔热层,每年能源消耗费用为8万元,即
,及若不建隔热层,每年能源消耗费用为8万元,即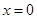 时,
时,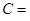
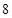 ,设
,设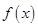 为隔热层建造费用与20年的能源消耗费用之和,每厘米厚的隔热层建造成本为6万元,厚度
为隔热层建造费用与20年的能源消耗费用之和,每厘米厚的隔热层建造成本为6万元,厚度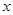 厘米的隔热层建造成本为
厘米的隔热层建造成本为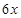 万元,建筑物每年的能源消耗费用
万元,建筑物每年的能源消耗费用 (单位:万元)与隔热层厚度
(单位:万元)与隔热层厚度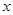 (单位:
(单位: )满足关系:
)满足关系: 20年的能源消耗费用为
20年的能源消耗费用为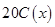 ,故
,故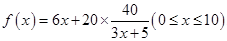 ;(Ⅱ)隔热层修建多厚时,总费用
;(Ⅱ)隔热层修建多厚时,总费用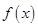 最小,并求最小值,由
最小,并求最小值,由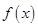 的解析式可知,
的解析式可知,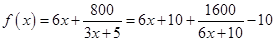 ,有基本不等式即可求出。
,有基本不等式即可求出。
试题解析:(Ⅰ)由题意,当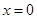 时,
时,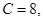 那么
那么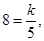 则
则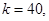 那么
那么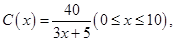
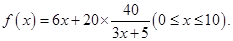
(Ⅱ)
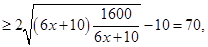
等号成立时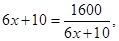 的
的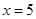 答:略.
答:略.
考点:应用题,基本不等式.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
某跨国饮料公司对全世界所有人均GDP(即人均纯收入)在0.5—8千美元的地区销售,该公司M饮料的销售情况的调查中发现:人均GDP处在中等的地区对该饮料的销售量最多,然后向两边递减.
(1)下列几个模拟函数中(x表示人均GDP,单位:千美元;y表示年人均M饮料的销量,单位:升),用哪个来描述人均,饮料销量与地区的人均GDP的关系更合适?说明理由.
A.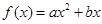 | B.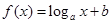 | C.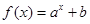 | D.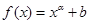 |
(3)因为M饮料在N国被检测出杀虫剂的含量超标,受此事件影响,M饮料在人均GDP不高于3千美元的地区销量下降5%,不低于6千美元的地区销量下降5%,其他地区的销量下降10%,根据(2)所求出的模拟函数,求在各个地区中,年人均M饮料的销量最多为多少?
 ,
,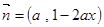 ,其中
,其中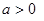 .函数
.函数 在区间
在区间 上有最大值为4,设
上有最大值为4,设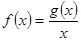 .
.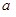 的值;
的值;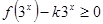 在
在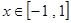 上恒成立,求实数
上恒成立,求实数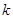 的取值范围.
的取值范围. 元.公司拟投入
元.公司拟投入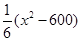 万元作为技改费用,投入50万元作为固定宣传费用,投入
万元作为技改费用,投入50万元作为固定宣传费用,投入 万元作为浮动宣传费用.试问:当该商品明年的销售量
万元作为浮动宣传费用.试问:当该商品明年的销售量 至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价.
至少应达到多少万件时,才可能使明年的销售收入不低于原收入与总投入之和?并求出此时商品的每件定价. 吨,此时所需生产费用为(
吨,此时所需生产费用为(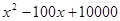 )万元,当出售这种商品时,每吨价格为
)万元,当出售这种商品时,每吨价格为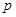 万元,这里
万元,这里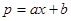 (
(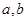 为常数,
为常数,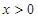 )
)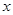 万件(假设该厂生产的产品全部销售),与年促销费用
万件(假设该厂生产的产品全部销售),与年促销费用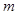 万元
万元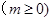 近似满足
近似满足 ,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).
,如果不促销,该产品的年销售量只能是1万件.已知2013年生产该产品的固定投入10万元,每生产1万件该产品需要再投入16万元.厂家将每件产品的销售价格规定为每件产品成本的1.5倍.(产品成本包括固定投入和再投入两部分资金).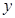 万元表示为年促销费用
万元表示为年促销费用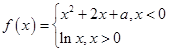 ,其中
,其中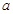 是实数,设
是实数,设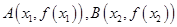 为该函数的图象上的两点,且
为该函数的图象上的两点,且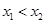 .
. 的单调区间;
的单调区间;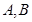 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求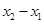 的最小值;
的最小值;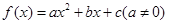 的图像顶点为
的图像顶点为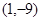 ,且图像在
,且图像在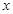 轴截得的线段长为6.
轴截得的线段长为6.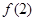 ;
; 在区间
在区间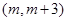 上单调,求
上单调,求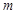 的范围.
的范围.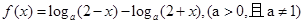
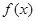 的奇偶性,并说明理由。
的奇偶性,并说明理由。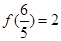 ,求使
,求使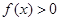 成立
成立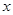 的集合。
的集合。