题目内容

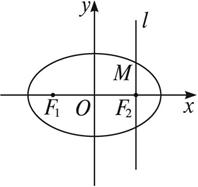
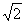在直角坐标系xOy中,设椭圆C:(a＞b＞0)的左、右两个焦点分别为F1、F2.过右焦点F2且与x轴垂直的直线l与椭圆C相交,其中一个交点为M(,1).

(1)求椭圆C的方程;

(2)设椭圆C的一个顶点为B(0,-b),直线BF2交椭圆C于另一点N,求△F1BN的面积.

 

【答案】

(1)

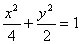
(2)

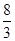
【解析】(1)解法一：∵l⊥x轴,

∴F2的坐标为(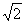,0).

由题意可知

∴所求椭圆方程为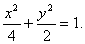

解法二:由椭圆定义,可知|MF1|+|MF2|=2a.

由题意|MF2|=1,∴|MF1|=2a-1.

又由Rt△MF1F2,可知(2a-1)2=(2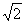)2+1,a＞0,

∴a=2.

又a2-b2=2,得b2=2.

∴椭圆C的方程为.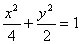

(2)解:直线BF2的方程为y=x-.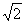

由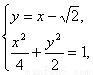得点N的纵坐标为.

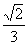又|F1F2|=2,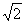

∴S△F1BN=.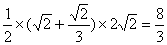

 

练习册系列答案
相关题目
在直角坐标系xOy中，椭圆C1：
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点分别为F1，F2．F2也是抛物线C2：y2=4x的焦点，点M为C1与C2在第一象限的交点，且|MF2|=
5
3
．
（Ⅰ）求C1的方程；
（Ⅱ）平面上的点N满足
MN
=
MF1
+
MF2
，直线l∥MN，且与C1交于A，B两点，若
OA
•
OB
=0，求直线l的方程．
在直角坐标系xOy中，已知点P（2cosx+1，2cos2x+2）和点Q（cosx，-1），其中x∈[0，π]．若向量
OP
与
OQ
垂直，求x的值．
精英家教网如图所示，在直角坐标系xOy中，射线OA在第一象限，且与x轴的正半轴成定角60°，动点P在射线OA上运动，动点Q在y轴的正半轴上运动，△POQ的面积为2
3
．
（1）求线段PQ中点M的轨迹C的方程；
（2）R1，R2是曲线C上的动点，R1，R2到y轴的距离之和为1，设u为R1，R2到x轴的距离之积．问：是否存在最大的常数m，使u≥m恒成立？若存在，求出这个m的值；若不存在，请说明理由．
在直角坐标系xOy中，已知圆M的方程为x2+y2-4xcosα-2ysinα+3cos2α=0（α为参数），直线l的参数方程为
x=tcosθ
y=1+tsinθ
(t为参数）
（I）求圆M的圆心的轨迹C的参数方程，并说明它表示什么曲线；
（II）求直线l被轨迹C截得的最大弦长．
在直角坐标系xOy中，已知椭圆C：
x2
a2
+
y2
b2
=1(a＞b＞0)的离心率e=
2
2
，左右两个焦分别为F1，F2．过右焦点F2且与x轴垂直的直线与椭圆C相交M、N两点，且|MN|=2．
（1）求椭圆C的方程；
（2）设椭圆C的一个顶点为B（0，-b），是否存在直线l：y=x+m，使点B关于直线l 的对称点落在椭圆C上，若存在，求出直线l的方程，若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网