题目内容
已知A,B,C是直线l上不同的三点,O是l外一点,向量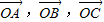 满足:
满足: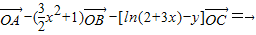 ,记y=f(x).
,记y=f(x).(1)求函数y=f(x)的解析式:
(2)若关于x的方程f(x)=2x+b在(0,1]上恰有两个不同的实根,求实数b的取值范围;
(3)若对任意
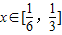 ,不等式|a-lnx|-ln[f′(x)-3x]>0恒成立,求实数a的取值范围.
,不等式|a-lnx|-ln[f′(x)-3x]>0恒成立,求实数a的取值范围.
【答案】分析:(1)由向量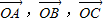 满足:
满足: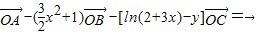 ,A,B,C在同一条直线上,知(
,A,B,C在同一条直线上,知(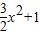 )+[ln(2+3x)-y]=1,由此能求出函数y=f(x)的解析式.
)+[ln(2+3x)-y]=1,由此能求出函数y=f(x)的解析式.
(2)由f(x)=2x+b,知b=f(x)-2x=ln(2+3x)+ -2x,令
-2x,令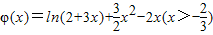 ,利用导数知识能求出b的取值范围.
,利用导数知识能求出b的取值范围.
(3)由已知的不等式解出a的取值范围并得到a的取值使不等式成立即可.
解答:解:(1)∵向量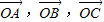 满足:
满足: ,
,
∴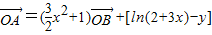
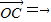 ,
,
又∵A,B,C在同一条直线上,
∴(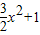 )+[ln(2+3x)-y]=1,
)+[ln(2+3x)-y]=1,
∴y=ln(2+3x)+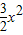 .
.
故f(x)=ln(2+3x)+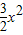 .…(3分)
.…(3分)
(2)∵f(x)=2x+b,f(x)=ln(2+3x)+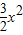 .
.
∴b=f(x)-2x=ln(2+3x)+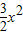 -2x,
-2x,
令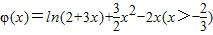 ,
,
则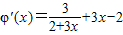 =
=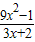 ,
,
∴当x∈(0, )时,φ'(x)<0;当
)时,φ'(x)<0;当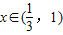 时,φ'(x)>0.
时,φ'(x)>0.
∵φ(0)=ln2,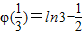 ,
,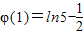 ,
,
ln5- -ln2=ln
-ln2=ln -
- =ln
=ln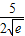 >0,
>0,
∴b∈(ln3- ,ln2).
,ln2).
∴b的取值范围是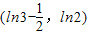 .…(8分)
.…(8分)
(3)由|a-lnx|-ln[f′(x)+3x]>0,
得a>lnx+ln3-ln(2+3x)或a<lnx-ln3+ln(2+3x),
设h(x)=lnx+ln3-ln(2+3x),g(x)=lnx-ln3+ln(2+3x)
依题意知a>h(x)或a<g(x)在x∈[ ,
, ]上恒成立,
]上恒成立,
∵h′(x)=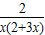 >0,g′(x)=
>0,g′(x)=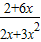 >0,
>0,
∴g(x)与h(x)都在[ ,
, ]上单增,要使不等式成立,
]上单增,要使不等式成立,
当且仅当a>h( )或a<g(
)或a<g( ),即a>ln
),即a>ln 或a<ln
或a<ln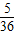 .…(14分)
.…(14分)
点评:本题考查学生利用向量、导数研究函数极值的能力,综合运用方程与函数的能力,以及求导数的能力.解题时要认真审题,注意等价转化思想的合理运用.
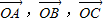 满足:
满足: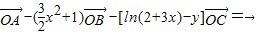 ,A,B,C在同一条直线上,知(
,A,B,C在同一条直线上,知(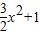 )+[ln(2+3x)-y]=1,由此能求出函数y=f(x)的解析式.
)+[ln(2+3x)-y]=1,由此能求出函数y=f(x)的解析式.(2)由f(x)=2x+b,知b=f(x)-2x=ln(2+3x)+
 -2x,令
-2x,令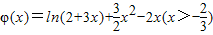 ,利用导数知识能求出b的取值范围.
,利用导数知识能求出b的取值范围.(3)由已知的不等式解出a的取值范围并得到a的取值使不等式成立即可.
解答:解:(1)∵向量
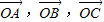 满足:
满足: ,
,∴
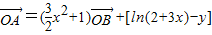
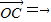 ,
,又∵A,B,C在同一条直线上,
∴(
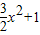 )+[ln(2+3x)-y]=1,
)+[ln(2+3x)-y]=1,∴y=ln(2+3x)+
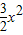 .
.故f(x)=ln(2+3x)+
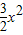 .…(3分)
.…(3分)(2)∵f(x)=2x+b,f(x)=ln(2+3x)+
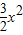 .
.∴b=f(x)-2x=ln(2+3x)+
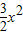 -2x,
-2x,令
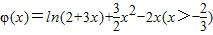 ,
,则
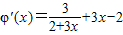 =
=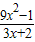 ,
,∴当x∈(0,
 )时,φ'(x)<0;当
)时,φ'(x)<0;当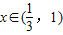 时,φ'(x)>0.
时,φ'(x)>0.∵φ(0)=ln2,
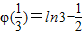 ,
,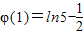 ,
,ln5-
 -ln2=ln
-ln2=ln -
- =ln
=ln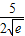 >0,
>0,∴b∈(ln3-
 ,ln2).
,ln2).∴b的取值范围是
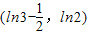 .…(8分)
.…(8分)(3)由|a-lnx|-ln[f′(x)+3x]>0,
得a>lnx+ln3-ln(2+3x)或a<lnx-ln3+ln(2+3x),
设h(x)=lnx+ln3-ln(2+3x),g(x)=lnx-ln3+ln(2+3x)
依题意知a>h(x)或a<g(x)在x∈[
 ,
, ]上恒成立,
]上恒成立,∵h′(x)=
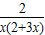 >0,g′(x)=
>0,g′(x)=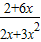 >0,
>0,∴g(x)与h(x)都在[
 ,
, ]上单增,要使不等式成立,
]上单增,要使不等式成立,当且仅当a>h(
 )或a<g(
)或a<g( ),即a>ln
),即a>ln 或a<ln
或a<ln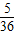 .…(14分)
.…(14分)点评:本题考查学生利用向量、导数研究函数极值的能力,综合运用方程与函数的能力,以及求导数的能力.解题时要认真审题,注意等价转化思想的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目