题目内容
7个排成一排,在下列情况下,各有多少种不同排法?
(1)甲排头;
(2)甲、乙、丙三人必须在一起;
(3)甲、乙、丙三人两两不相邻;
(4)甲不排头,乙不排当中.
(1)甲排头;
(2)甲、乙、丙三人必须在一起;
(3)甲、乙、丙三人两两不相邻;
(4)甲不排头,乙不排当中.
(1)甲固定不动,其余有
=720,即共有
=720种;…(3分)
(2)先排甲、乙、丙三人,有
,再把该三人当成一个整体,再加上另四人,相当于5人的全排列,即
,则共有
=720种;…(6分)
(3)先排甲、乙、丙之外的四人,有
,四人形成五个空位,甲、乙、丙三人排
这五个空位,有
,则共有
=1440种;…(10分)
(4)不考虑限制条件有
,而甲排头有
,乙排当中有
,这样重复了甲排头,乙排当中
一次,即
-2
+
=3720…(14分)
| A | 66 |
| A | 66 |
(2)先排甲、乙、丙三人,有
| A | 33 |
| A | 55 |
| A | 55 |
| A | 33 |
(3)先排甲、乙、丙之外的四人,有
| A | 44 |
这五个空位,有
| A | 35 |
| A | 35 |
| A | 44 |
(4)不考虑限制条件有
| A | 77 |
| A | 66 |
| A | 66 |
| A | 55 |
| A | 77 |
| A | 66 |
| A | 55 |

练习册系列答案
相关题目
 中的
中的 ,且
,且 互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )
互不相同,在所有这些方程所表示的曲线中,不同的抛物线共有( )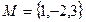 ,
,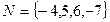 从两个集合中各取一个
从两个集合中各取一个