题目内容
定义域为R的函数 ,若关于
,若关于 的方程
的方程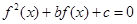 恰有5个不同的实数解
恰有5个不同的实数解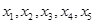 ,则
,则 ( )
( )
A.4 B.10 C.12 D.16
【答案】
B
【解析】
试题分析:画出函数 的图象,
的图象,

它关于x=2对称,函数值域为(0,+∞)。
因为关于 的方程
的方程 恰有5个不同的实数解
恰有5个不同的实数解 ,令
,令 ,所以关于t的方程
,所以关于t的方程 ,应有两正根,且t=1或t>0且t
,应有两正根,且t=1或t>0且t 1.
1.
所以 ,即
,即 10,故选B。
10,故选B。
考点:本题主要考查分段函数的解析式求法及其图象的作法;根的存在性及根的个数判断.
点评:画出函数 的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有5个不同的整数解
的图象,根据图象我们可以判断出关于x的方程f2(x)+bf(x)+c=0有5个不同的整数解 时,所满足的条件是解答本题的关键.
时,所满足的条件是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 . ,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 .
,若关于x的方程f2(x)+bf(x)+c=0有3个不同的整数解x1,x2,x3,则x12+x22+x32等于 . ,若关于
,若关于 的方程
的方程 有3个不同的实根,则关于x的不等式
有3个不同的实根,则关于x的不等式 的解集为( )
的解集为( ) D. (c,1)
D. (c,1) ,若关于
,若关于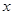 的方程
的方程 有3个不同的实根
有3个不同的实根 ,则
,则 等于
等于 C. 13 D.
C. 13 D. 