题目内容
 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,-| π |
| 2 |
| π |
| 2 |
(1)求函数f(x)的表达式;
(2)若f(α)+f(α-
| π |
| 3 |
| 24 |
| 25 |
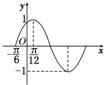
分析:(1)根据函数的图象,求出A、T,求出ω,函数x=-
时,y=0,结合-
<φ<
求出φ,然后求函数f(x)的表达式;
(2)利用f(α)+f(α-
)=
,化简出(sinα+cosα)2,2sinαcosα=
>0且α为△ABC的一个内角,确定sinα>0,cosα>0,求sinα+cosα的值.
| π |
| 6 |
| π |
| 2 |
| π |
| 2 |
(2)利用f(α)+f(α-
| π |
| 3 |
| 24 |
| 25 |
| 24 |
| 25 |
解答:解:(1)从图知,函数的最大值为1,则A=1.
函数f(x)的周期为T=4×(
+
)=π.
而T=
,则ω=2.又x=-
时,y=0,
∴sin[2×(-
)+φ]=0.
而-
<φ<
,则φ=
,
∴函数f(x)的表达式为f(x)=sin(2x+
).
(2)由f(α)+f(α-
)=
,得
sin(2α+
)+sin(2α-
)=
,
即2sin2αcos
=
,∴2sinαcosα=
.
∴(sinα+cosα)2=1+
=
.
∵2sinαcosα=
>0,α为△ABC的内角,
∴sinα>0,cosα>0,即sinα+cosα>0.∴sinα+cosα=
.
函数f(x)的周期为T=4×(
| π |
| 12 |
| π |
| 6 |
而T=
| 2π |
| ω |
| π |
| 6 |
∴sin[2×(-
| π |
| 6 |
而-
| π |
| 2 |
| π |
| 2 |
| π |
| 3 |
∴函数f(x)的表达式为f(x)=sin(2x+
| π |
| 3 |
(2)由f(α)+f(α-
| π |
| 3 |
| 24 |
| 25 |
sin(2α+
| π |
| 3 |
| π |
| 3 |
| 24 |
| 25 |
即2sin2αcos
| π |
| 3 |
| 24 |
| 25 |
| 24 |
| 25 |
∴(sinα+cosα)2=1+
| 24 |
| 25 |
| 49 |
| 25 |
∵2sinαcosα=
| 24 |
| 25 |
∴sinα>0,cosα>0,即sinα+cosα>0.∴sinα+cosα=
| 7 |
| 5 |
点评:本题是基础题,考查函数解析式的求法,根据三角函数式,确定函数的取值范围,是解题的难点,考查学生视图能力,计算能力.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目