题目内容
已知函数f(x)=loga(x+1),若函数y=g(x)的图象上任意一点P关于原点的对称点Q的轨迹恰好是函数f(x)的图象:(1)写出g(x)的解析式
(2)记F(x)=f(x)+g(x),讨论F(x)的单调性
(3)若a>1,x∈[0,1)时,总有F(x)=f(x)+g(x)≥m成立,求实数m的取值范围.
【答案】分析:(1)由已知可得函数f(x)=loga(x+1)与函数y=g(x)的图象关于原点对称,进而利用坐标法,可得g(x)的解析式
(2)根据F(x)=f(x)+g(x),结合(1)的结论,求出F(x)的解析式,利用导数法,求出内函数的单调性,结合对数函数的单调性与复合函数同增异减的原则,可分析出F(x)的单调性
(3)若a>1,x∈[0,1)此时结合(2)的结论,可得函数为增函数,若F(x)=f(x)+g(x)≥m恒成立,仅须F(x)的最小值,大于等于m即可.
解答:解:(1)设P(x,y)是函数y=g(x)图象上的任意一点
则P关于原点的对称点Q的坐标为(-x,-y)
∵已知点Q在函数f(x)的图象上
∴-y=f(-x),而f(x)=loga(x+1)
∴-y=loga(-x+1)
∴y=-loga(-x+1)
而P(x,y)是函数y=g(x)图象上的点
∴y=g(x)=-loga(-x+1)=-loga(1-x)
(2)F(x)=f(x)+g(x)=loga(x+1)-loga(1-x)=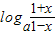 ,
,
则函数F(x)=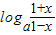 的定义域为(-1,1),
的定义域为(-1,1),
令h(x)=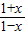 ,则h′(x)=
,则h′(x)= ,
,
∵当x∈(-1,1)时,h′(x)≥0恒成立
故h(x)=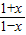 在(-1,1)上单调递增,
在(-1,1)上单调递增,
当0<a<1时,y=logat为减函数,此时F(x)=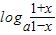 为减函数,
为减函数,
当a>1时,y=logat为增函数,此时F(x)=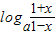 为增函数.
为增函数.
(3)由(2)得若a>1
当x∈[0.1)时,F(x)=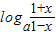 为增函数
为增函数
此时F(x)min=F(0)=loga1=0
∴m≤0
∴所求m的取值范围:m≤0
点评:本题考查的知识点是函数恒成立问题,函数解析式的求法,函数单调性的判断与证明,是函数图象和性质的综合应用,难度中档.
(2)根据F(x)=f(x)+g(x),结合(1)的结论,求出F(x)的解析式,利用导数法,求出内函数的单调性,结合对数函数的单调性与复合函数同增异减的原则,可分析出F(x)的单调性
(3)若a>1,x∈[0,1)此时结合(2)的结论,可得函数为增函数,若F(x)=f(x)+g(x)≥m恒成立,仅须F(x)的最小值,大于等于m即可.
解答:解:(1)设P(x,y)是函数y=g(x)图象上的任意一点
则P关于原点的对称点Q的坐标为(-x,-y)
∵已知点Q在函数f(x)的图象上
∴-y=f(-x),而f(x)=loga(x+1)
∴-y=loga(-x+1)
∴y=-loga(-x+1)
而P(x,y)是函数y=g(x)图象上的点
∴y=g(x)=-loga(-x+1)=-loga(1-x)
(2)F(x)=f(x)+g(x)=loga(x+1)-loga(1-x)=
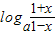 ,
,则函数F(x)=
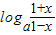 的定义域为(-1,1),
的定义域为(-1,1),令h(x)=
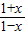 ,则h′(x)=
,则h′(x)= ,
,∵当x∈(-1,1)时,h′(x)≥0恒成立
故h(x)=
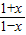 在(-1,1)上单调递增,
在(-1,1)上单调递增,当0<a<1时,y=logat为减函数,此时F(x)=
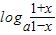 为减函数,
为减函数,当a>1时,y=logat为增函数,此时F(x)=
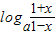 为增函数.
为增函数.(3)由(2)得若a>1
当x∈[0.1)时,F(x)=
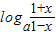 为增函数
为增函数此时F(x)min=F(0)=loga1=0
∴m≤0
∴所求m的取值范围:m≤0
点评:本题考查的知识点是函数恒成立问题,函数解析式的求法,函数单调性的判断与证明,是函数图象和性质的综合应用,难度中档.

练习册系列答案
相关题目