题目内容
已知函数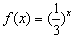
，函数
，
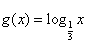（1）若g（mx2+2x+m）的定义域为R，求实数m的取值范围；
（2）当x∈[-1，1]时，求函数y=[f（x）]2-2a f（x）+3的最小值h（a）；
（3）是否存在非负实数m、n，使得函数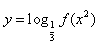
的定义域为[n，m]，值域为[2n，2m]，若存在，求出m、n的值；若不存在，则说明理由。
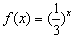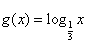，函数，（1）若g（mx2+2x+m）的定义域为R，求实数m的取值范围；
（2）当x∈[-1，1]时，求函数y=[f（x）]2-2a f（x）+3的最小值h（a）；
（3）是否存在非负实数m、n，使得函数
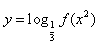的定义域为[n，m]，值域为[2n，2m]，若存在，求出m、n的值；若不存在，则说明理由。 解：（1）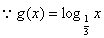
，
，
令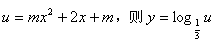
，
当m=0时，u=2x，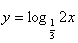
的定义域为（0，+∞），不成立；
当m≠0时，
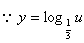的定义域为R，
，
解得m＞1；
综上所述，m＞1。
（2）
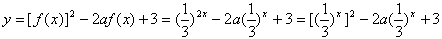，x∈[-1，1]，
令
，
，
对称轴为t=a，
当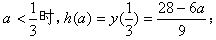
当
；
当a＞3时，
；
综上所述，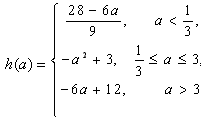
；
（3）
，
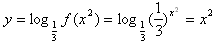假设存在，
由题意，知
，
∴存在n=0，m=2，使得函数
的定义域为[0，2]，值域为[0，4]。
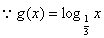，，令
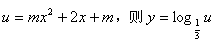，当m=0时，u=2x，
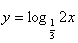的定义域为（0，+∞），不成立； 当m≠0时，
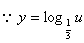的定义域为R，，解得m＞1；
综上所述，m＞1。
（2）
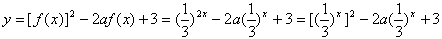，x∈[-1，1]，令
，，对称轴为t=a，
当
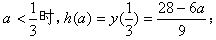
当
；当a＞3时，
；综上所述，
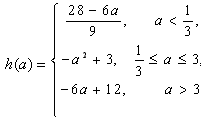；（3）
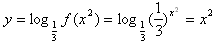，假设存在，
由题意，知
，∴存在n=0，m=2，使得函数
的定义域为[0，2]，值域为[0，4]。 
练习册系列答案
同步练习强化拓展系列答案
相关题目
已知函数f（x）的定义域为[-1，5]，部分对应值如下表，f（x）的导函数y=f′（x）的图象如图所示，给出关于f（x）的下列命题：
)=－1,当且仅当0<x<1时f(x)<0,且对任意x、y∈(－1,1)都有f(x)+f(y)=f(
),试证明：w.w.w.k.s.5.u.c.o.m 
