题目内容
已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜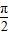
=的图象在y轴上的截距为1，在相邻两最值点（x，2），（x+
，-2）处分别取得最大值和最小值，则函数f（x）的解析式为 ．
【答案】分析：易知A=2，利用相邻两最值点之间为半个周期，求出ω，最后由曲线过点（0，1）求出φ．
解答：解：由已知，A=2，
=x+
-x=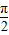
，T=π，∴ω=2．又曲线过点（0，1）∴1=2sinφ，φ=
．
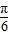故答案为：f（x）=2sin（2x+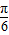
）
点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，数形结合的思想．准确掌握三角函数的图象和性质是前提．要能借助图形，提取有用的信息来解决问题，本题有用的信息为：函数的周期及函数的最值，根据此信息确定出A，ω及φ的值是解本题的关键．
解答：解：由已知，A=2，
=x+-x=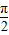，T=π，∴ω=2．又曲线过点（0，1）∴1=2sinφ，φ=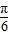．故答案为：f（x）=2sin（2x+
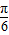）点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，数形结合的思想．准确掌握三角函数的图象和性质是前提．要能借助图形，提取有用的信息来解决问题，本题有用的信息为：函数的周期及函数的最值，根据此信息确定出A，ω及φ的值是解本题的关键．
练习册系列答案
相关题目