题目内容
【题目】已知正项等比数列![]() ,等差数列
,等差数列![]() 满足
满足![]() ,且
,且![]() 是
是![]() 与
与![]() 的等比中项.
的等比中项.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
【答案】(1)![]() ;(2)
;(2) .
.
【解析】试题分析:(1)根据![]() ,
,![]() 是
是![]() 与
与![]() 的等比中项列出关于公比
的等比中项列出关于公比![]() 、公差
、公差![]() 的方程组,解方程组可得
的方程组,解方程组可得![]() 与
与![]() 的值,从而可得数列
的值,从而可得数列![]() 与
与![]() 的的通项公式;(2)由(1)可知
的的通项公式;(2)由(1)可知![]() ,所以
,所以![]() ,对
,对![]() 分奇数、偶数两种情况讨论,分别利用分组求和法,错位相减求和法,结合等差数列求和公式与等比数列求和公式求解即可.
分奇数、偶数两种情况讨论,分别利用分组求和法,错位相减求和法,结合等差数列求和公式与等比数列求和公式求解即可.
试题解析:(1)设等比数列![]() 的公比为
的公比为![]() ,等差数列
,等差数列![]() 的公差为
的公差为![]()
由![]() 是
是![]() 与
与![]() 的等比中项可得:
的等比中项可得: ![]()
又![]() ,则:
,则: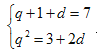 ,解得
,解得![]() 或
或![]()
因为![]() 中各项均为正数,所以
中各项均为正数,所以![]() ,进而
,进而![]() .
.
故![]() .
.
(2)设![]()
设数列![]() 的前
的前![]() 项和为
项和为![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,
,
当![]() 为偶数时,
为偶数时,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ,
,
而 ![]() ①,
①,
则![]() ②,
②,
由①-②得:
![]()
![]() ,
,
![]() ,因此
,因此![]() , 综上:
, 综上: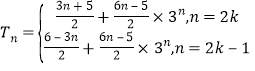 .
.

练习册系列答案
相关题目
【题目】已知某保险公司的某险种的基本保费为![]() (单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如下表:
上年度出险次数 | 0 | 1 | 2 | 3 |
|
保费(元) |
|
|
|
|
|
随机调查了该险种的200名续保人在一年内的出险情况,得到下表:
出险次数 | 0 | 1 | 2 | 3 |
|
频数 | 140 | 40 | 12 | 6 | 2 |
该保险公司这种保险的赔付规定如下表:
出险序次 | 第1次 | 第2次 | 第3次 | 第4次 | 第5次及以上 |
赔付金额(元) |
|
|
|
| 0 |
将所抽样本的频率视为概率。
(1)求本年度—续保人保费的平均值的估计值;
(2)求本年度—续保人所获赔付金额的平均值的估计值;
(3)据统计今年有100万投保人进行续保,若该公司此险种的纯收益不少于900万元,求![]() 的最小值(纯收益=总入保额-总赔付额)。
的最小值(纯收益=总入保额-总赔付额)。