题目内容
1.已知x∈R,若“x≥a”是“$\sqrt{x}$有意义”的充分不必要条件,则实数a的取值范围是a>0.分析 问题转化为“x≥a”是“x≥0”的充分不必要条件,从而求出a的范围.
解答 解:若“x≥a”是“$\sqrt{x}$有意义”的充分不必要条件,
则“x≥a”是“x≥0”的充分不必要条件,
则实数a>0,
故答案为:a>0.
点评 本题考查了充分必要条件,考查二次根式的性质,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
12.已知函数f(x)=$\frac{1}{3}$x3-(4m-1)x2+(15m2-2m-7)x+2在R上是增函数,则m的取值范围为( )
| A. | m≤2或m≥4 | B. | -4≤m≤-2 | C. | 2≤m≤4 | D. | 以上皆不对 |
16.已知O是△ABC内部一点,$\overrightarrow{OA}$+$\overrightarrow{OB}$+$\overrightarrow{OC}$=$\overrightarrow{0}$,$\overrightarrow{AB}$•$\overrightarrow{AC}$=6,∠BAC=60°,则△OBC的面积为( )
| A. | 3$\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 3 |
6.若函数y=2exsinx,则y′=( )
| A. | -2excosx | B. | 2ex(sinx-cosx) | C. | -2exsinx | D. | 2ex(sinx+cosx) |
10.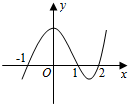 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
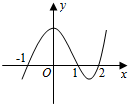 设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )
设函数f(x)在R上可导,其导函数为f′(x),且函数y=(2-x)f′(x)的图象如图所示,则下列结论中一定成立的是( )| A. | 函数f(x)有极大值f(1)和极小值f(-1) | B. | 函数f(x)有极大值f(1)和极小值f(2) | ||
| C. | 函数f(x)有极大值f(2)和极小值f(1) | D. | 函数f(x)有极大值f(-1)和极小值f(2) |