题目内容
已知函数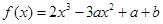 (其中a,b为实常数)。
(其中a,b为实常数)。
(Ⅰ)讨论函数 的单调区间:
的单调区间:
(Ⅱ)当 时,函数
时,函数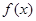 有三个不同的零点,证明:
有三个不同的零点,证明: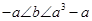 :
:
(Ⅲ)若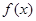 在区间
在区间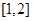 上是减函数,设关于x的方程
上是减函数,设关于x的方程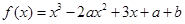 的两个非零实数根为
的两个非零实数根为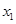 ,
,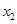 。试问是否存在实数m,使得
。试问是否存在实数m,使得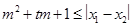 对任意满足条件的a及t
对任意满足条件的a及t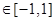 恒成立?若存在,求m的取值范围;若不存在,请说明理由。
恒成立?若存在,求m的取值范围;若不存在,请说明理由。
(I)当a=0时,f(x)的增区间为(-∞,+∞);
当a>0时,f(x)的增区间为(-∞,0),(a,+∞);f(x)的减区间为(0,a);
当a<0时,f(x)的增区间为(-∞,a),(0,+∞);f(x)的减区间为(a,0).
(II)-a<b<a3-a.(III)存在实数m满足条件,此时m∈[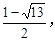
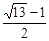 ].
].
解析试题分析:(I)求导函数,对参数a进行讨论,利用导数的正负,确定函数的单调区间;
(II)确定f(x)的极大值为f(0)=a+b,f(x)的极小值为f(a)=a+b-a3,要使f(x)有三个不同的零点,则f(0)>0,f(a)<0,从而得证;
(III)先确定|x1-x2|=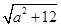 ,并求得其最小值,假设存在实数m满足条件,则m2+tm+1≤(
,并求得其最小值,假设存在实数m满足条件,则m2+tm+1≤(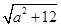 )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,从而可求m的范围.
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,从而可求m的范围.
解:(I)∵ 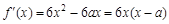 ,
,
当a=0时, ≥0,于是
≥0,于是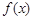 在R上单调递增;
在R上单调递增;
当a>0时,x∈(0,a),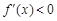 ,得
,得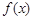 在(0,a)上单调递减;
在(0,a)上单调递减;
x∈(-∞,0)∪(a,+∞),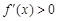 ,得
,得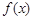 在(-∞,0),(a,+∞)上单调递增;
在(-∞,0),(a,+∞)上单调递增;
当a<0时,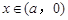 ,
,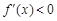 ,得
,得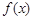 在(0,a)上单调递减;
在(0,a)上单调递减;
x∈(-∞,a)∪(0,+∞),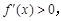 得
得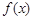 在(-∞,a),(0,+∞)上单调递增.
在(-∞,a),(0,+∞)上单调递增.
综上所述:当a=0时,f(x)的增区间为(-∞,+∞);
当a>0时,f(x)的增区间为(-∞,0),(a,+∞);f(x)的减区间为(0,a);
当a<0时,f(x)的增区间为(-∞,a),(0,+∞);f(x)的减区间为(a,0).……3分
(II)当a>0时,由(I)得f(x)在(-∞,0),(a,+∞)上是增函数,f(x)在(0,a)上是减函数;则f(x)的极大值为f(0)=a+b,f(x)的极小值为f(a)=a+b-a3.
要使f(x)有三个不同的零点,则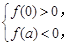 即
即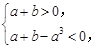 可得-a<b<a3-a.…8分
可得-a<b<a3-a.…8分
(III)由2x3-3ax2+a+b=x3-2ax2+3x+a+b,得x3-ax2-3x=0即x(x2-ax-3)=0,
由题意得x2-ax-3=0有两非零实数根x1,x2,则x1+x2=a,x1x2=-3,
即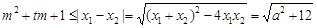 .∵ f (x)在[1,2]上是减函数,
.∵ f (x)在[1,2]上是减函数,
∴ 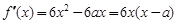 ≤0在[1,2]上恒成立,
≤0在[1,2]上恒成立,
其中x-a≤0即x≤a在[1,2]上恒成立,∴ a≥2.∴ 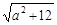 ≥4.
≥4.
假设存在实数m满足条件,则m2+tm+1≤(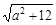 )min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,
)min,即m2+tm+1≤4,即m2+tm-3≤0在t∈[-1,1]上恒成立,
∴ 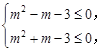 解得
解得 .
.
∴ 存在实数m满足条件,此时m∈[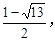
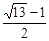 ]. …………………14分
]. …………………14分
考点:本题主要考查导数知识的运用,考查函数的单调性,考查分类讨论的数学思想,考查函数的极值与最值,考查恒成立问题,综合性强.
点评:解决该试题的关键是利用导数的正负对于函数单调性的影响得到函数单调区间,进而分析极值问题,以及构造函数的思想求证函数的最值,解决恒成立问题的运用。

 阅读快车系列答案
阅读快车系列答案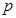 与每日生产产品件数
与每日生产产品件数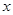 (
(
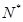 )间的关系为
)间的关系为 ,每生产一件正品盈利4000元,每出现一件次品亏损2000元.
,每生产一件正品盈利4000元,每出现一件次品亏损2000元.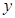 (元)表示成日产量
(元)表示成日产量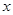 (单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当2
(单位:辆/千米)的函数。当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当2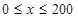 时,车流速度v是车流密度x的一次函数.
时,车流速度v是车流密度x的一次函数.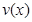 的表达式;
的表达式;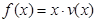 可以达到最大,并求出最大值(精确到1辆/小时).
可以达到最大,并求出最大值(精确到1辆/小时). 在点
在点 处取得极小值-4,使其导函数
处取得极小值-4,使其导函数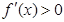 的
的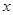 的取值范围为(1,3)
的取值范围为(1,3) 的解析式及
的解析式及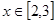 时,求
时,求 的最大值。
的最大值。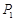 (元)和
(元)和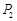 (元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.
(元)分别记小王先后两次买米时,该品种大米的单价,请问:仅这两次买米而言,甲、乙两种购买方式,从平均单价考虑,哪种比较合算?请进行探讨,并给出探讨过程.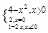
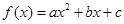 的零点是-1和3,当
的零点是-1和3,当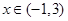 时,
时,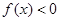 ,且
,且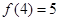 。(1)求该二次函数的解析式;(2)求函数
。(1)求该二次函数的解析式;(2)求函数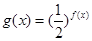 的最大值。
的最大值。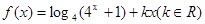 是偶函数
是偶函数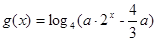 ,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。
,若函数f(x)与g(x)的图像有且只有一个公共点,求实数a的取值范围。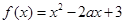
 的单调递减区间(—∞,2],求函数
的单调递减区间(—∞,2],求函数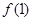 的最大值.
的最大值.