题目内容
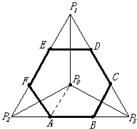 设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是
设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是
- A.三角形区域
- B.四边形区域
- C.五边形区域
- D.六边形区域
D
分析:本题考查的知识点是二元一次不等式(组)与平面区域,要求集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},表示的平面区域的形状,我们要先根据集合中点P满足的性质,找出所表示区域的边界,进而判断出区域各边界围成的图形形状.
解答: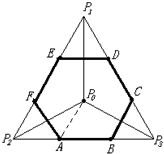 解:如图,A、B、C、D、E、F为各边三等分点,
解:如图,A、B、C、D、E、F为各边三等分点,
若|PP0|=|PPi|
当i=1时,P点落在P1P0的垂直平分线上,又由P∈D,故P点的轨迹为ED;
当i=2时,P点落在P2P0的垂直平分线上,又由P∈D,故P点的轨迹为AF;
当i=3时,P点落在P3P0的垂直平分线上,又由P∈D,故P点的轨迹为BC;
故满足条件集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},
则集合S表示的平面区域是六边形ABCDEF,
故选D
点评:本题主要考查集合与平面几何基础知识.本题主要考查阅读与理解、信息迁移以及学生的学习潜力,考查学生分析问题和解决问题的能力.属于创新题型.
分析:本题考查的知识点是二元一次不等式(组)与平面区域,要求集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},表示的平面区域的形状,我们要先根据集合中点P满足的性质,找出所表示区域的边界,进而判断出区域各边界围成的图形形状.
解答:
 解:如图,A、B、C、D、E、F为各边三等分点,
解:如图,A、B、C、D、E、F为各边三等分点,若|PP0|=|PPi|
当i=1时,P点落在P1P0的垂直平分线上,又由P∈D,故P点的轨迹为ED;
当i=2时,P点落在P2P0的垂直平分线上,又由P∈D,故P点的轨迹为AF;
当i=3时,P点落在P3P0的垂直平分线上,又由P∈D,故P点的轨迹为BC;
故满足条件集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},
则集合S表示的平面区域是六边形ABCDEF,
故选D
点评:本题主要考查集合与平面几何基础知识.本题主要考查阅读与理解、信息迁移以及学生的学习潜力,考查学生分析问题和解决问题的能力.属于创新题型.

练习册系列答案
相关题目
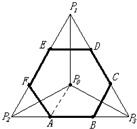 8、设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是( )
8、设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是( )