题目内容
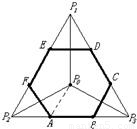
8、设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心.若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是
六边形区域
.分析:由集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则P点应位于P0Pi的三条垂直平分线之内,又由D是正△P1P2P3及其内部的点构成的集合,我们易画出满足条件的图象,并判断其形状.
解答: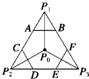 解:如图所示,AB、CD、EF分别为P0P1、P0P2、P0P3的垂直平
解:如图所示,AB、CD、EF分别为P0P1、P0P2、P0P3的垂直平
分线,且AB、CD、EF分别交P1P2、P2P3、P3P1于点A、C、D、E、
F、B.若|PP0|=|PP1|,则点P在线段AB上,若|PP0|≤|PP1|,则点P在
梯形ABP3P2中.
同理,若|PP0|≤|PP2|,则点P在梯形CDP3P1中.
若|PP0|≤|PP3|,则点P在梯形EFP1P2中.
综上可知,若|PP0|≤|PPi|,i=1,2,3,则点P在六边形ABFEDC中.
故答案为:六边形区域
 解:如图所示,AB、CD、EF分别为P0P1、P0P2、P0P3的垂直平
解:如图所示,AB、CD、EF分别为P0P1、P0P2、P0P3的垂直平分线,且AB、CD、EF分别交P1P2、P2P3、P3P1于点A、C、D、E、
F、B.若|PP0|=|PP1|,则点P在线段AB上,若|PP0|≤|PP1|,则点P在
梯形ABP3P2中.
同理,若|PP0|≤|PP2|,则点P在梯形CDP3P1中.
若|PP0|≤|PP3|,则点P在梯形EFP1P2中.
综上可知,若|PP0|≤|PPi|,i=1,2,3,则点P在六边形ABFEDC中.
故答案为:六边形区域
点评:本题考查的知识点是不等式表示的平面区域,根据|PP0|≤|PPi|,画出满足条件的图形是解答本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
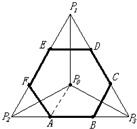 8、设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是( )
8、设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是( )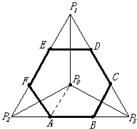 设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是
设D是正△P1P2P3及其内部的点构成的集合,点P0是△P1P2P3的中心,若集合S={P|P∈D,|PP0|≤|PPi|,i=1,2,3},则集合S表示的平面区域是