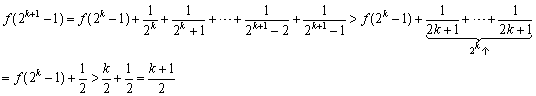设.由.f(3)>1..f(15)>2.- (1)你能得到怎样的结论?并证明, (2)是否存在一个正数T.使对任意的自然数n.恒有f(n)<T成立?并证明你的结论. 题目和参考答案——青夏教育精英家教网—

题目内容

设，由，f(3)>1，，f(15)>2，…

（1）你能得到怎样的结论？并证明；

（2）是否存在一个正数T，使对任意的自然数n，恒有f(n)<T成立？并证明你的结论。

答案：
解析：

数列1，3，7，15，…。通项公式为a_n=2ⁿ-1，数列，1，，2，…通项公式为，∴ 猜想：。

证明：（1）当n=1时，不等式成立。

（2）假设当n=k时不等式成立，即。则

∴ 当n=k+1时不等式也成立。

据（1）、（2）对任何nÎN*原不等式均成立。

（2）对任意给定的正意T，设它的整数部分为T¢，记m=T¢+1，则m>T。由（1）知：f(2^2m-1)>m，∴ f(2^2m-1)>T，这说明，对任意给定的正数T，总能找到正整数n（如可取假设中n为2m），使得f(n)>T。∴ 不存在正数T，使得对任意的正整数n，总有f(n)<T成立。

练习册系列答案

．
（Ⅰ）求ω的值；
（Ⅱ）若函数y=g（x）的图象是由y=f（x）的图象向右平移

个单位长度得到，求y=g（x）的单调增区间．

设函数f（x）=（sinωx+cosωx）²+2cos²ωx（ω＞0）的最小正周期为

2π

．
（1）求ω的值；
（2）当x∈[0，

]时，求f（x）的最值．
（3）若函数y=g（x）的图象是由y=f（x）的图象向右平移

个单位长度得到，求y=g（x）的单调增区间．

设f，g都是由A到A的映射，其对应法则如下表（从上到下）：
表1映射f的对应法则

X	1	2	3	4
f（x）	3	4	2	1

表2映射g的对应法则

x	1	2	3	4
g（x）	4	3	1	2

设f，g 都是由A到A的映射（其中A={1，2，3}），其对应法则如下表，则f[g（3）]等于（　　）

g：x→y	x	1	2	3
g：x→y	y	3	2	1
f：x→y	x	1	2	3
f：x→y	y	1	1	2

设f，g都是由A到A的映射，其对应法则如下表（从上到下）：
表1 映射f的对应法则

原像	1	2	3	4
像	3	4	2	1

表2 映射g的对应法则

原像	1	2	3	4
像	4	3	1	2

试题分类