Question

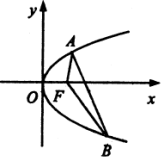
直线l与抛物线y²＝4x交于两点A、B，O为坐标原点，且

(1)求证：直线l恒过一定点；

(2)若，求直线l的斜率k的取值范围；

(3)设抛物线的焦点为F，∠AFB＝θ，试问θ角能否等于120°？若能，求出相应的直线l的方程；若不能，请说明理由．

Answer 1

答案：
解析：

(1)若直线l与x轴不垂直，设其方程为，l与抛物线的交点坐标分别为、，由得，即， 　　则又由得． 　　则即，则直线l的方程为， 　　则直线l过定点(2，0)． 　　若直线l与x轴垂直，易得l的方程为x＝2， 　　则l也过定点(2，0)． 　　综上，直线l恒过定点(2，0)． 　　(2)由(1)得，可得解得k的取值范围是 　　(3)假定，则有，如图，即 　　由(1)得.由定义得从而有 　　 　　均代入(*)得 　　，即这与相矛盾． 　　经检验，当轴时，．故