题目内容
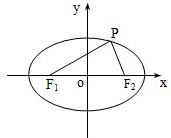 已知点P在椭圆
已知点P在椭圆| x2 |
| 49 |
| y2 |
| 24 |
(1)|PF1|•|PF2|
(2)△PF1F2的面积.
分析:(1)根据椭圆的方程,算出a=5且焦距|F1F2|=2c=10.设|PF1|=m,|PF2|=n,根据椭圆的定义和勾股定理建立关于m、n的方程组,平方相减即可求出|PF1|•|PF2|=48;
(2)根据(1)的结论,结合直角三角形的面积公式,可得△PF1F2的面积S=
|PF1|•|PF2|=24,得到本题答案.
(2)根据(1)的结论,结合直角三角形的面积公式,可得△PF1F2的面积S=
| 1 |
| 2 |
解答:解:(1)∵椭圆方程为
+
=1,
∴a2=49,b2=24,可得c2=a2-b2=25,即a=7,c=5
设|PF1|=m,|PF2|=n,则有
由(1)2-(2),得2mn=96,即mn=48,
∴|PF1|•|PF2|=48
(2)由(1),可得|PF1|•|PF2|=48,
∵PF1⊥PF2,得∠F1PF2=90°
∴△PF1F2的面积S=
|PF1|•|PF2|=
×48=24.
| x2 |
| 49 |
| y2 |
| 24 |
∴a2=49,b2=24,可得c2=a2-b2=25,即a=7,c=5
设|PF1|=m,|PF2|=n,则有
|
由(1)2-(2),得2mn=96,即mn=48,
∴|PF1|•|PF2|=48
(2)由(1),可得|PF1|•|PF2|=48,
∵PF1⊥PF2,得∠F1PF2=90°
∴△PF1F2的面积S=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题给出椭圆的焦点三角形为直角三角形,求它的面积,着重考查了勾股定理、椭圆的定义和简单几何性质等知识,属于基础题.

练习册系列答案
相关题目
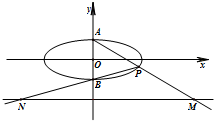 在平面直角坐标系xOy中,如图,已知椭圆C:
在平面直角坐标系xOy中,如图,已知椭圆C: