题目内容
设椭圆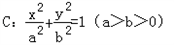 的一个顶点与抛物线
的一个顶点与抛物线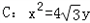 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率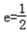 ,且过椭圆右焦点F2的直线l与椭圆C交于M、N两点。
,且过椭圆右焦点F2的直线l与椭圆C交于M、N两点。
(1)求椭圆C的方程;
(2)是否存在直线l,使得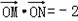 ,若存在,求出直线l的方程;若不存在,说明理由。
,若存在,求出直线l的方程;若不存在,说明理由。
(3)若AB是椭圆C经过原点O的弦,MN∥AB,求证: 为定值。
为定值。
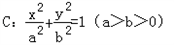 的一个顶点与抛物线
的一个顶点与抛物线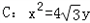 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率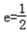 ,且过椭圆右焦点F2的直线l与椭圆C交于M、N两点。
,且过椭圆右焦点F2的直线l与椭圆C交于M、N两点。(1)求椭圆C的方程;
(2)是否存在直线l,使得
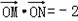 ,若存在,求出直线l的方程;若不存在,说明理由。
,若存在,求出直线l的方程;若不存在,说明理由。(3)若AB是椭圆C经过原点O的弦,MN∥AB,求证:
 为定值。
为定值。解:抛物线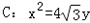 的焦点为
的焦点为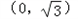
∵椭圆 的一个顶点与抛物线
的一个顶点与抛物线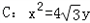 的焦点重合
的焦点重合
∴椭圆的一个顶点为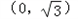 ,
,
即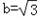
∵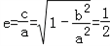 ,
,
∴a=2,
∴椭圆的标准方程为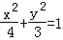 ;
;
(2)解:由题可知,椭圆的右焦点为(1,0),直线l与椭圆必相交
①当直线斜率不存在时,M(1, ),N(1,-
),N(1,- ),
),
∴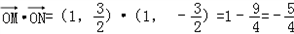 ,不合题意;
,不合题意;
②设存在直线l为y=k(x-1)(k≠0),且M(x1,y1),N(x2,y2)
由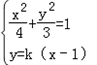 得(3+4k2)x2-8k2x+4k2-12=0,
得(3+4k2)x2-8k2x+4k2-12=0,
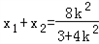 ,
,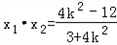 ,
,
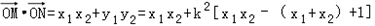
=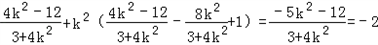
所以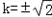 ,
,
故直线l的方程为 或
或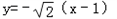 ;
;
(3)证明:设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(2)可得:|MN|=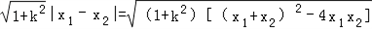
=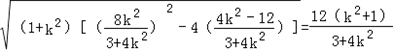
由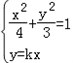 消去y,
消去y,
并整理得: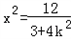 ,
,
|AB|=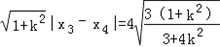 ,
,
∴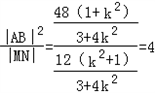 为定值 。
为定值 。
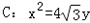 的焦点为
的焦点为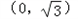
∵椭圆
 的一个顶点与抛物线
的一个顶点与抛物线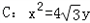 的焦点重合
的焦点重合∴椭圆的一个顶点为
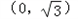 ,
,即
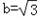
∵
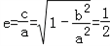 ,
,∴a=2,
∴椭圆的标准方程为
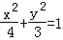 ;
;(2)解:由题可知,椭圆的右焦点为(1,0),直线l与椭圆必相交
①当直线斜率不存在时,M(1,
 ),N(1,-
),N(1,- ),
),∴
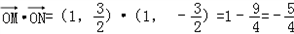 ,不合题意;
,不合题意;②设存在直线l为y=k(x-1)(k≠0),且M(x1,y1),N(x2,y2)
由
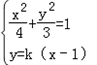 得(3+4k2)x2-8k2x+4k2-12=0,
得(3+4k2)x2-8k2x+4k2-12=0,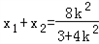 ,
,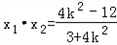 ,
,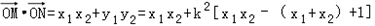
=
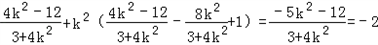
所以
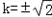 ,
,故直线l的方程为
 或
或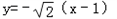 ;
;(3)证明:设M(x1,y1),N(x2,y2),A(x3,y3),B(x4,y4)
由(2)可得:|MN|=
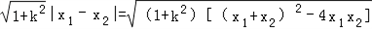
=
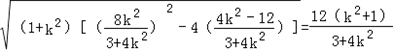
由
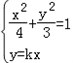 消去y,
消去y,并整理得:
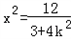 ,
,|AB|=
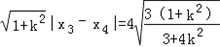 ,
,∴
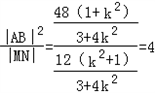 为定值 。
为定值 。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
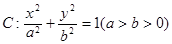 的一个顶点与抛物线
的一个顶点与抛物线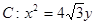 的焦点重合,
的焦点重合,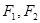 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率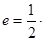 且过椭圆右焦点
且过椭圆右焦点 的直线
的直线 与椭圆C交于
与椭圆C交于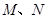 两点.
两点.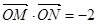 .若存在,求出直线
.若存在,求出直线 AB,求证:
AB,求证: 为定值
为定值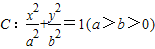 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率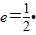 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.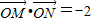 .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由.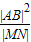 为定值.
为定值. 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点. .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由. 为定值.
为定值.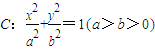 的一个顶点与抛物线
的一个顶点与抛物线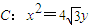 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率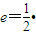 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.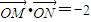 .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由.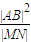 为定值.
为定值.