题目内容
设椭圆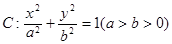 的一个顶点与抛物线
的一个顶点与抛物线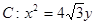 的焦点重合,
的焦点重合,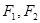 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率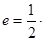 且过椭圆右焦点
且过椭圆右焦点 的直线
的直线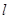 与椭圆C交于
与椭圆C交于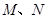 两点.
两点.
(1)求椭圆C的方程;
(2)是否存在直线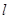 ,使得
,使得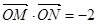 .若存在,求出直线
.若存在,求出直线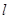 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(3)若AB是椭圆C经过原点O的弦,
MN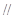 AB,求证:
AB,求证: 为定值
为定值
【答案】
解:椭圆的顶点为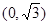 ,即
,即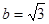
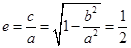 ,解得
,解得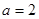 ,
, 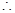 椭圆的标准方程为
椭圆的标准方程为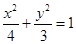 …… 3分
…… 3分
(2)由题可知,直线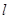 与椭圆必相交.
与椭圆必相交.
①当直线斜率不存在时,经检验不合题意.
②设存在直线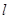 为
为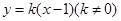 ,且
,且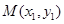 ,
,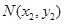 .
.
由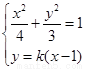 得
得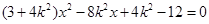 ,
,
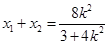 ,
,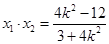 ,
,
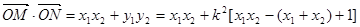
=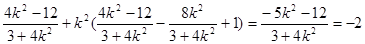
所以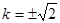 ,故直线
,故直线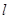 的方程为
的方程为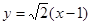 或
或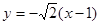 …………8分
…………8分
(3)设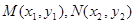 ,
,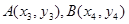
由(2)可得: |MN|=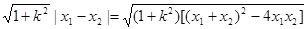
=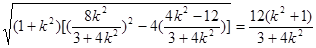 .
.
由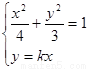 消去y,并整理得:
消去y,并整理得: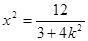 ,
,
|AB|=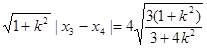 ,∴
,∴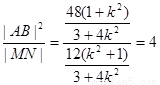 为定值
为定值
【解析】略

练习册系列答案
 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
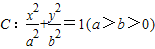 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率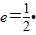 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.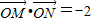 .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由.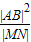 为定值.
为定值. 的一个顶点与抛物线
的一个顶点与抛物线 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点. .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由. 为定值.
为定值.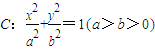 的一个顶点与抛物线
的一个顶点与抛物线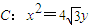 的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率
的焦点重合,F1,F2分别是椭圆的左、右焦点,且离心率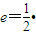 且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.
且过椭圆右焦点F2的直线l与椭圆C交于M、N两点.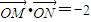 .若存在,求出直线l的方程;若不存在,说明理由.
.若存在,求出直线l的方程;若不存在,说明理由.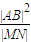 为定值.
为定值.