题目内容

下列命题为真命题的个数（　　）
①若命题p：?x∈R，x2-x-1＞0则￢p：?x∈R，x2-x-1≤0
②要得到y=sin(2x+
π
3
)的图象，可以将y=sinx横坐标变为原来的2倍向左移动
π
3

③y=sin(2x+
π
3
)，(x∈(
π
6
，
π
2
)的值域为(-
3
2
，1)
④x＜1函数y=x+
1
x-1
的值域（-∞，-1]．
分析：根据特称命题的否定方法，求出命题p的否定，可判断①；根据函数图象的变换法则，求出y=sinx横坐标变为原来的2倍向左移动
π
3
的解析式，可判断②；根据正弦型函数的图象和性质，求出函数的值域，可判断③；利用基本不等式，求出函数y=x+
1
x-1
的值域，可判断④
解答：解：若命题p：?x∈R，x2-x-1＞0则￢p：?x∈R，x2-x-1≤0，故①为真命题；
将y=sinx横坐标变为原来的2倍可得y=sin
1
2
x的图象，再向左移动
π
3
可得：y=sin
1
2
（x+
π
3
）=y=sin(
1
2
x+
π
6
)的图象，故②为假命题；
当x∈(
π
6
，
π
2
)时，(2x+
π
3
)∈(
2π
3
，
4π
3
)，当(2x+
π
3
)=
2π
3
时，函数取最大值
3
2
，当(2x+
π
3
)=
4π
3
时，函数取最小值-
3
2
，
故函数y=sin(2x+
π
3
)，x∈(
π
6
，
π
2
)的值域为(-
3
2
，
3
2
)，故③为假命题；
④当x＜1时，x-1＜0，函数y=x+
1
x-1
=x-1+
1
x-1
+1≤-2+1=-1，故函数y=x+
1
x-1
的值域（-∞，-1]，故④为真命题；
故真命题的个数有2个
故选：B
点评：本题以命题的真假判断为载体考查了特称命题的否定，图象的变换法则，函数的值域，是函数图象和性质的综合应用，难度中档．
练习册系列答案
相关题目
已知命题p：?x∈（-∞，0），2x＜3x，命题q：?x∈(0，
π
2
)，tanx＞sinx，则下列命题为真命题的是（　　）
①．p∧q；②．p∨（?q）；③．（?p）∧q；④．p∧（?q）
A、1个B、2个C、3个D、4个
（2012•厦门模拟）定义在R上的函数f（x），其图象是连续不断的，如果存在非零常数λ（λ∈R，使得对任意的x∈R，都有f（x+λ）=λf（x），则称y=f（x）为“倍增函数”，λ为“倍增系数”，下列命题为真命题的是
①③④
①③④
（写出所有真命题对应的序号）．
①若函数y=f（x）是倍增系数λ=-2的倍增函数，则y=f（x）至少有1个零点；
②函数f（x）=2x+1是倍增函数，且倍增系数λ=1；
③函数f(x)=
e
-x
 
是倍增函数，且倍增系数λ∈（0，1）；
④若函数f（x）=sin（2ωx）（ω＞0）是倍增函数，则ω=
kπ
2
(k∈N*)．
给出下列命题：
①有两个面平行，其余各面都是平行四边形所围成的几何体一定是棱柱；
②有一个面是多边形，其余各面都是三角形所围成的几何体是棱锥；
③用一个平行于棱锥底面的平面去截棱锥，得到的几何体叫棱台．
以上命题中真命题的个数为（　　）
已知三个不同的平面α，β，γ，a，b，c分别为平面α，β，γ内的直线，若β⊥γ且α与γ相交但不垂直，则下列命题为真命题的是
④⑥
④⑥
．
①?b?β，b⊥γ     ②?b?β，b∥γ    ③?a?α，a⊥γ
④?a?α，a∥γ     ⑤?c?γ，c∥α    ⑥?c?γ，c⊥β

下列命题是真命题的序号为：             

①定义域为R的函数，对都有，则为偶函数

②定义在R上的函数，若对，都有，则函数的图像关于中心对称

③函数的定义域为R，若与都是奇函数，则是奇函数

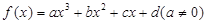③函数的图形一定是对称中心在图像上的中心对称图形。

⑤若函数有两不同极值点，若，且，则关于的方程的不同实根个数必有三个.

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网