题目内容
已知三个命题：①关于x的方程x2+mx+2m=0无实数根；②关于x的不等式|x+2|+|x-3|＞m对于任意的x∈R恒成立；③函数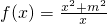
在[-2，0）上单调递减．如果上述三个命题中两真一假，那么实数m的取值范围是
- A.（-2，0）∪（2，8）
- B.（-2，0]∪（5，8）∪[9，+∞）
- C.（-∞，-2）∪（5，8）
- D.（-∞，-2]∪（0，2）∪[5，8）
D
分析：分别求三个命题为真时的m的范围，由三个命题中两真一假，分三类情况来分析都可得到m的范围，然后取并集即可得到答案．
解答：①关于x的方程x2+mx+2m=0无实数根，则△=m2-8m＜0，解得0＜m＜8；
②关于x的不等式|x+2|+|x-3|＞m对于任意的x∈R恒成立，则m＜（|x+2|+|x-3|）min=5；
③函数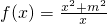在[-2，0）上单调递减，则f′（x）=
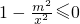在x∈[-2，0）上恒成立，
即m2≥x2在x∈[-2，0）上恒成立，只需m2≥（x2）max=4，故m≤-2，或m≥2．
上述三个命题中两真一假，则（0，8）∩（-∞，5）∩（-2，2）=（0，2），
或（0，8）∩[5，+∞）∩[（-∞，-2]∪[2，+∞）]=[5，8），
或[（-∞，0]∪[8，+∞）]∩（-∞，5）∩[（-∞，-2]∪[2，+∞）]=（-∞，-2]．
故m的取值范围为：（-∞，-2]∪（0，2）∪[5，8）．
故选D．
点评：本题为求实数的取值范围，涉及函数的单调性，恒成立问题以及一元二次方程根的情况，属基础题．
分析：分别求三个命题为真时的m的范围，由三个命题中两真一假，分三类情况来分析都可得到m的范围，然后取并集即可得到答案．
解答：①关于x的方程x2+mx+2m=0无实数根，则△=m2-8m＜0，解得0＜m＜8；
②关于x的不等式|x+2|+|x-3|＞m对于任意的x∈R恒成立，则m＜（|x+2|+|x-3|）min=5；
③函数
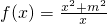在[-2，0）上单调递减，则f′（x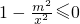）=在x∈[-2，0）上恒成立，即m2≥x2在x∈[-2，0）上恒成立，只需m2≥（x2）max=4，故m≤-2，或m≥2．
上述三个命题中两真一假，则（0，8）∩（-∞，5）∩（-2，2）=（0，2），
或（0，8）∩[5，+∞）∩[（-∞，-2]∪[2，+∞）]=[5，8），
或[（-∞，0]∪[8，+∞）]∩（-∞，5）∩[（-∞，-2]∪[2，+∞）]=（-∞，-2]．
故m的取值范围为：（-∞，-2]∪（0，2）∪[5，8）．
故选D．
点评：本题为求实数的取值范围，涉及函数的单调性，恒成立问题以及一元二次方程根的情况，属基础题．
练习册系列答案
相关题目