题目内容
已知圆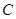 过点
过点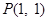 ,且与圆
,且与圆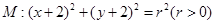 关于直线
关于直线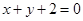 对称.
对称.
(1)求圆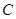 的方程;
的方程;
(2)设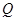 为圆
为圆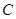 上一个动点,求
上一个动点,求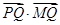 的最小值;
的最小值;
(3)过点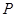 作两条相异直线分别与圆
作两条相异直线分别与圆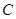 相交于
相交于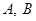 ,且直线
,且直线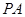 和
和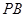 直线的倾斜角互补,
直线的倾斜角互补,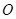 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和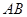 是否平行,并说明理由.
是否平行,并说明理由.
【答案】
见解析.
【解析】第一问中,利用设圆心坐标,然后利用圆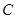 过点
过点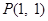 ,且与圆
,且与圆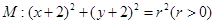 关于直线
关于直线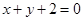 对称.
对称.
则可得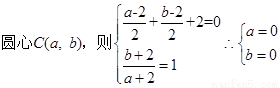
得到圆的方程。
第二问中,
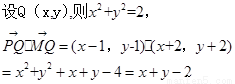 利用坐标法求解。
利用坐标法求解。
第三问中,设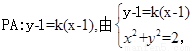 得到关于A点的横坐标,同理可得B的横坐标,然后借助于直线方程,和斜率公式求解得到。
得到关于A点的横坐标,同理可得B的横坐标,然后借助于直线方程,和斜率公式求解得到。
解:设
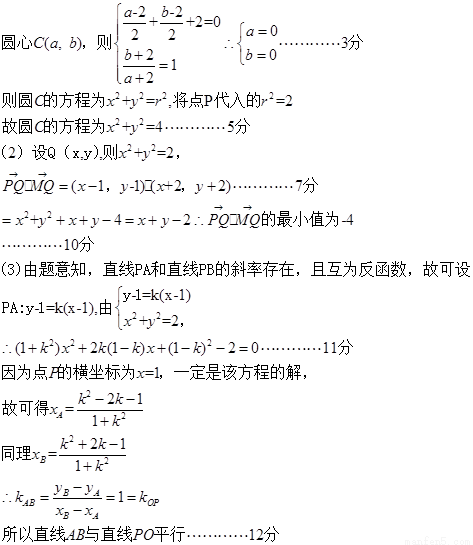

练习册系列答案
相关题目
 过点
过点 ,且与圆
,且与圆 相内切.
相内切. (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D,与双曲线
,D,与双曲线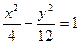 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 过点
过点 ,且与圆
,且与圆 相内切.
相内切.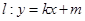 (其中
(其中 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,
,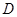 ,与双曲线
,与双曲线 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线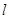 ,使得向量
,使得向量 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由. 过点
过点 ,且与圆
,且与圆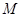 :
: 关于直线
关于直线 对称.
对称. 为圆
为圆 的最小值;
的最小值; 作两条相异直线分别与圆
作两条相异直线分别与圆 ,且直线
,且直线 和直线
和直线 的倾斜角互补,
的倾斜角互补, 为坐标原点,试判断直线
为坐标原点,试判断直线 和
和 是否平行?请说明理由.
是否平行?请说明理由.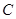 过点
过点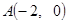 ,且与圆
,且与圆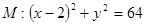 相内切.
相内切.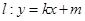 (其中
(其中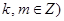 与(1)中所求轨迹交于不同两点
与(1)中所求轨迹交于不同两点 ,D,与双曲线
,D,与双曲线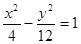 交于不同两点
交于不同两点 ,问是否存在直线
,问是否存在直线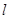 ,使得向量
,使得向量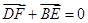 ,若存在,指出这样的直线有多少条?若不存在,请说明理由.
,若存在,指出这样的直线有多少条?若不存在,请说明理由.