Question

已知二次函数f(x)满足:①在x=1时有极值;②图象过点(0,-3),且在该点处的切线与直线2x+y=0平行.

(1)求f(x)的解析式;

(2)求函数g(x)=f(x²)的单调递增区间.

Answer 1

分析：本题考查利用导数研究函数的性质.

解：(1)设f(x)=ax²+bx+c,则f′(x)=2ax+b.

由题设可得   

解得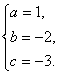.所以f(x)=x²-2x-3.        

(2)g(x)=f(x²)=x⁴-2x²-3,g′(x)=4x³-4x=4x(x-1)(x+1).

列表:

x	(-∞,-1)	-1	(-1,0)	0	(0,1)	1	(1,+∞)
f′(x)	-	0	+	0	-	0	+
f(x)

由表可得:函数g(x)的单调递增区间为(-1,0),(1,+∞).