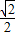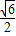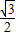题目内容
过椭圆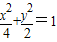 的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )A.
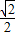
B.
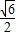
C.

D.
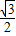
【答案】分析:根据已知中椭圆的标准方程,我们可以求出A,B两点的坐标,结合双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,将A,B坐标代入即可求出双曲线的离心率.
解答:解:由已知中椭圆的标准方程为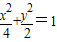
我们可以求出A(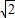 ,1),B(
,1),B(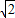 ,-1),
,-1),
设双曲线为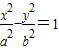 (a>0,b>0),
(a>0,b>0),
渐近线方程为y=±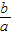 x,因为A、B在渐近线上,
x,因为A、B在渐近线上,
所以1=
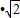
∴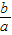 =
=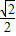
∴e=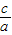 =
=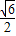
故选B
点评:本题考查的知识点是椭圆及双曲线的几何特征,其中求出AB的坐标,并根据双曲线的性质,求出双曲线实半轴长a和虚半轴长b的比例关系是解答本题的关键.
解答:解:由已知中椭圆的标准方程为
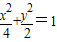
我们可以求出A(
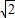 ,1),B(
,1),B(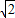 ,-1),
,-1),设双曲线为
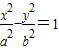 (a>0,b>0),
(a>0,b>0),渐近线方程为y=±
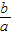 x,因为A、B在渐近线上,
x,因为A、B在渐近线上,所以1=

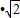
∴
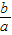 =
=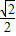
∴e=
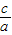 =
=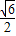
故选B
点评:本题考查的知识点是椭圆及双曲线的几何特征,其中求出AB的坐标,并根据双曲线的性质,求出双曲线实半轴长a和虚半轴长b的比例关系是解答本题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
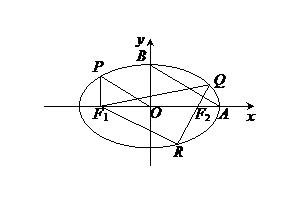 (2)过右焦点
(2)过右焦点 的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是



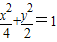 的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )
的右焦点作x轴的垂线交椭圆于A、B两点,已知双曲线的焦点在x轴上,对称中心在坐标原点且两条渐近线分别过A、B两点,则双曲线的离心率是( )