题目内容
【题目】已知点![]() 的坐标分别为
的坐标分别为![]() ,直线
,直线![]() 相交于点
相交于点![]() ,且它们的斜率之积是
,且它们的斜率之积是![]() ,点
,点![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
(Ⅰ)求![]() 的方程;
的方程;
(Ⅱ)过点![]() 作直线
作直线![]() 交曲线
交曲线![]() 于
于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,若
点,若![]() ,
, ![]() ,证明:
,证明: ![]() 为定值.
为定值.
【答案】(Ⅰ)![]() ; (Ⅱ)
; (Ⅱ)![]() .
.
【解析】试题分析:
(Ⅰ)设出动点![]() 坐标为
坐标为![]() ,把斜率之积用坐标表示出来化简可得
,把斜率之积用坐标表示出来化简可得![]() 的方程(注意有些点不合要求);
的方程(注意有些点不合要求);
(Ⅱ)解析几何中的定值问题,设点![]() 的坐标分别为
的坐标分别为![]() .由
.由![]() ,可求得
,可求得![]() ,并代入曲线
,并代入曲线![]() 的方程,得
的方程,得![]() 的方程,同理得
的方程,同理得![]() 的方程,这样发现
的方程,这样发现![]() 是方程
是方程![]() 的两个实数根,由韦达定理可得
的两个实数根,由韦达定理可得![]() .
.
试题解析:
(Ⅰ)设点![]() ,由已知得
,由已知得![]() ,
,
化简得点![]() 的轨迹
的轨迹![]() 的方程:
的方程: ![]() .
.
(Ⅱ)设点![]() 的坐标分别为
的坐标分别为![]() .
.
由![]() ,所以
,所以![]() ,
,
所以 ![]()
因为点![]() 在曲线
在曲线![]() 上,所以
上,所以 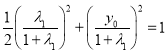 ,
,
化简得![]() ①,
①,
同理,由![]() 可得:
可得: ![]() ,
,
代入曲线![]() 的方程得
的方程得 ![]() ②,
②,
由①②得![]() 是方程
是方程![]() 的两个实数根(△>0),
的两个实数根(△>0),
所以![]() .
.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目